Um refrigerador internamente reversível tem um coeficiente de performance modificado em função dos processos reais de transferência de calor determinado por
em que é a taxa de resfriamento do refrigerador, é a taxa de rejeição de calor e é a alimentação de potência. Mostre que pode ser representado em termos das temperaturas dos reservatórios e, das resistências térmicas nos lados quente e frio, e, por
sendo. Mostre também que a alimentação de potência pode ser representada por
Passo 1
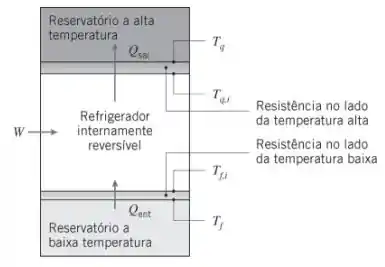
Bora para mais uma questão juntos 😊. Aqui, nós temos um refrigerador passando por um processo de troca térmica. Ilustrativamente, temos:
E nós queremos provar as equações do coeficiente de performance e do trabalho desse refrigerador. Então vamos lá!
Passo 2
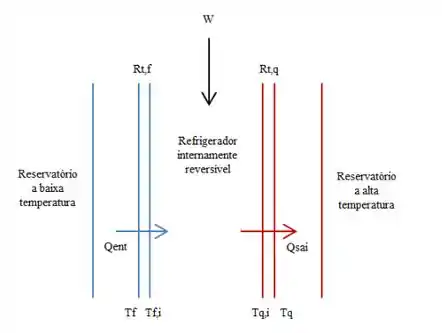
Vamos provar primeiro a equação do coeficiente de performance, beleza? Pela imagem acima, olhando as paredes do refrigerador e usando as resistências térmicas das paredes do lado quente e frio, temos:
Reescrevendo as equações, para as temperaturas internas ficamos com:
Em que as resistências do lado quente e frio são dadas pela relação com a resistência total das duas paredes:
E a taxa de calor que sai pode ser expresso por:
Podemos substituir essa informação na equação da temperatura interna do lado e quente e ficamos com:
Como,
Então,
Por consequência:
Passo 3
Agora que já manipulamos todas as expressões que precisávamos, podemos substituir:
e
Em,
Ficando com:
Show! Agora é só resolver essa equação algebricamente e vamos chegar ao resultado desejado para o coeficiente de performance do refrigerador.
Passo 4
Como o trabalho que deve ser consumido pelo refrigerador é dado pela equação do calor consumido na parte fria e o coeficiente de performance.
Podemos substitui a equação do coeficiente de performance do refrigerador e ficar com:
Resposta
Ei, a resposta está no passo a passo :)