Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 31
Para refrigerar uma casa de verão sem usar um ciclo de refrigeração por compressão de vapor, ar é passado por um tubo plástico (, , ), que está submerso em um corpo de água próximo à casa. A temperatura da água no corpo de água é de e um coeficiente convectivo de é mantido na superfície externa do tubo.
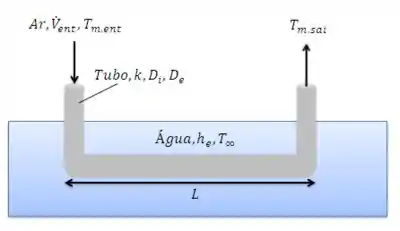
Se o ar vindo da casa entra no tubo com uma temperatura de e a uma vazão volumétrica , qual comprimento do tubo é necessário para se ter uma temperatura na sua saída de ? Qual é a potência do soprador necessária para passar o ar através do comprimento do tubo, sendo sua superfície interna lisa?
Passo 1
Vamos começar esquematizando a situação. Temos ar a uma vazão de e temperatura entrando um tubo submerso em água a uma temperatura de . Sabendo que a água proporciona um coeficiente convectivo externo de devemos encontrar qual é o comprimento de tubo necessário para que o ar saia resfriado a . Tudo bem?
Vamos começar analisando os mecanismos de transferência de calor envolvidos no processo. Teremos convecção externa entre a água e a superfície do tubo, condução na parede do tubo e convecção interna entre a parede interna da tubulação e o ar. Como temos vários mecanismos ocorrendo é conveniente expressar a taxa de transferência de calor em termos do coeficiente global:
Também iremos considerar que não há perdas de energia. Ou seja, toda a taxa de transferência de calor serve apenas para resfriar o ar. Então:
Passo 2
Abrindo o termo teremos:
Deixando o termo em função da área interna do cilindro:
Temos agora uma expressão para obter o comprimento do tubo. Mas para isso, precisaremos antes calcular o coeficiente global . Vamos a ele.
Passo 3
O coeficiente global é calculado como:
Como queremos o coeficiente global em relação à área interna:
Para este problema temos três resistências térmicas envolvidas: convecção interna, condução e convecção interna. Para um duto cilíndrico elas são dadas por:
Antes de fazer a soma das resistências precisaremos calcular o coeficiente convectivo interno. Como primeiro passo, vamos transformar a vazão volumétrica de entrada em vazão mássica:
O ar entra a . Nesta temperatura, de acordo com a tabela A-4 do apêndice A:
Então,
Nosso próximo passo será calcular a temperatura média do ar e reunir suas propriedades nesta temperatura. A temperatura média é dada por:
Para esta temperatura:
A partir destes dados iremos calcular o coeficiente convectivo médio no interior da tubulação.
Passo 4
O próximo passo é o cálculo do número de Reynolds:
Como , o escoamento é turbulento.
Para escoamento turbulento no interior de dutos cilíndricos:
Voltando para a equação do coeficiente global:
Passo 5
Agora que encontramos que temos o coeficiente global podemos utilizá-lo para definir o comprimento da tubulação:
Para finalizar o exercpcio temos ainda que calcular a potência do soprador necessária. A potência é dada por:
Em que é a perda de carga devido ao escoamento. A perda de carga na tubulação pode ser calculada por:
Então, precisamos ainda calcular o fator de atrito e a velocidade de escoamento. O fator de atrito pode ser estimado através do número de Reynolds pela relação:
E avelocidade média é calculada a partir da vazão volumética por:
Substituindo na relação de potência:
Resposta
e .