Um produto alimentício líquido é processado em um esterilizador de fluxo contínuo. O líquido entra no esterilizador a uma temperatura e a uma vazão de e , respectivamente. Uma restrição tempo-temperatura requer que o produto seja mantido a uma temperatura média de por para matar bactérias, enquanto a segunda restrição é que a temperatura local do produto não pode exceder , de modo a preservar um gosto agradável. O esterilizador é constituído por uma primeira seção de aquecimento, , caracterizada por um fluxo térmico uniforme, uma seção intermediária de esterilização que é isolada termicamente, e uma terceira seção, onde há resfriamento, com comprimento . A seção de resfriamento, é composta por um tubo não isolado exposto a um ambiente, sem vento, a . O tubo do esterilizador tem parede delgada com diâmetro . As propriedades do alimento são similares às da água líquida a .

(a) Qual fluxo térmico é necessário na seção de aquecimento para garantir uma temperatura média do produto máxima de ?

(b) Determine a localização e o valor da temperatura local do produto máxima. A segunda restrição é satisfeita?

(c) Determine o comprimento mínimo da seção de esterilização necessário para satisfazer a restrição tempo-temperatura.

(d) Esboce a distribuição axial das temperaturas média, na superfície e na linha central, da entrada da seção de aquecimento até a saída da seção de resfriamento.

Vamos agora para o item (b). Precisamos definir onde ocorre a temperatura máxima do produto.

Pela configuração do equipamento, podemos perceber que a temperatura do produto só irá aumentar durante a seção de aquecimento, até atingir uma temperatura máxima que irá se manter na zona de esterilização, que é isolada. A última seção é de resfriamento, então a partir dela a temperatura do produto deve diminuir. Portanto, devemos ter a temperatura máxima ao final da zona de aquecimento.

Além disso, o calor para aquecer o fluido vem das paredes, então, é esperado que a temperatura máxima seja atingida na superfície do tubo. Juntando estas duas informações, o ponto de temperatura máxima será no final da zona de aquecimento, na superfície do tubo.

Ainda no item (b), devemos obter a temperatura máxima. Para isso, vamos começar considerando que só há transferência de calor por convecção. Então:

Chegamos a uma relação para obter a temperatura máxima, porém, ainda precisamos obter o coeficiente convectivo para este processo.

Para encontrar , nosso próximo passo será calcular o número de Reynolds:

Como , o regime de escoamento é turbulento.

Para regime turbulento no interior de dutos cilíndricos:

Substituindo na relação de temperatura:

Como podemos ver . Então, a restrição de temperatura máxima é satisfeita.

Começaremos agora o item (c). Neste item, devemos obter o comprimento da seção de esterilização.

A restrição ligada a esta parte do equipamento é de que o produto deve ser mantido por . Sabemos que o fluido escoa com vazão , então sua velocidade de escoamento no interior da tubulação é:

Então, para que o fluido se mantenha na zona de esterilização, o comprimento deve ser de :

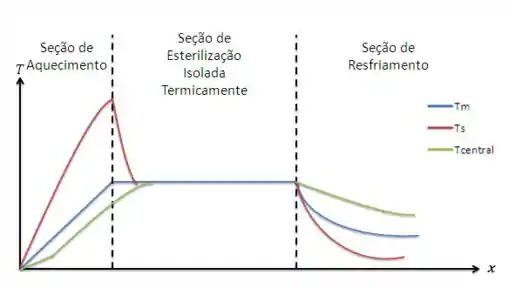
Por fim, o item (d) nos pede para esboçar as temperaturas média, na superfície e central para as três seções.

Vamos começar descrevendo qual é o comportamento esperado. Na zona de aquecimento, como dissemos anteriormente, o fluxo é proveniente da superfície do tubo, então, é de esperar que a temperatura da superfície seja a mais alta, além de possuir a maior taxa de crescimento. Por outro lado, a linha central é o ponto mais afastado da superfície, então, espera-se que a temperatura neste ponto seja a mais baixa, além de ser a que cresce com a menor taxa.

Na seção de esterilização temos que a parede da tubulação é isolada. Ou seja, não há transferência de calor entre o produto e o ambiente externo. Então, o esperado é que a temperatura média se mantenha constante, com as temperaturas da superfície e da linha central se aproximando do valor médio.

Na seção de resfriamento, teremos um comportamento análogo ao que discutimos na seção de aquecimento. Porém, desta vez a temperatura da superfície será a menor, por estar em contato com o ar frio e também terá a taxa de decrescimento de temperatura mais rápida. Em relação à temperatura da linha central, desta vez será a temperatura mais alta observada e a que resfria mais devagar, devido à ser o ponto mais afastado da superfície.

Então, as curvas de temperatura devem ser parecidas com: