Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 32

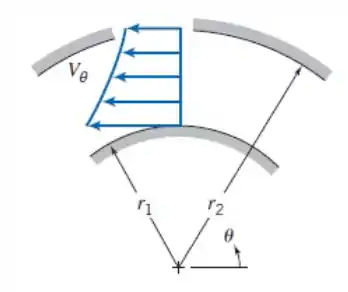
Repita o Exemplo 6.1, porém com uma consideração um pouco mais realista de que o escoamento é similar a um perfil de vórtice livre (irrotacional), Vθ = c/r (em que c é uma constante), como mostrado na Fig. P6.32. Fazendo isso, prove que a vazão é dada por Q = k ∆ p   , em que k é

k = w ln ⁡ r 2 r 1 2 r 2 2 r 1 2 ρ r 2 2 - r 1 2

E w é a profundidade da curva.

Passo 1

Pessoal, nesta questão temos um escoamento curvo, muito parecido com o Exemplo resolvido 6.1 do livro. Vamos então aplicar a equação de Euler através da linha de corrente (note que a direção normal é a direção r):

∂ p ∂ r = ρ V 2 r

Temos as seguintes considerações:

-escoamento sem atrito;

-escoamento incompressível;

-escoamento uniforma na seção.

A distribuição de pressão será dada por:

d p = ∂ p ∂ r d r

Substituindo V θ = c r   e integrando, ficamos com:

d p = ρ V θ 2 r d r

∫ p 1 p 2 d p = ∫ r 1 r 2 ρ c 2 r 3 d r

∆ p = ρ c 2 - 1 2 r 2 r 2 r 1

∆ p = - ρ c 2 2 1 r 2 2 - 1 r 1 2

∆ p = - ρ c 2 r 1 2 - r 2 2 2 r 1 2 r 2 2  

∆ p = ρ c 2 r 2 2 - r 1 2 2 r 1 2 r 2 2

Passo 2

A equação da vazão é definida por:

Q = ∫ V → ∙ d A   →

Onde a área é dada por d A = w   d r . Substituindo a velocidade e a área, ficamos com:

Q = ∫ r 1 r 2 c r w d r

Q = c w ln ⁡ r 2 - ln ⁡ r 1

Q = c w ln ⁡ r 2 r 1

Isolando a constante c temos:

c = Q w ln ⁡ r 2 r 1

Passo 3

Agora vamos fazer a substituição de c na equação da variação de pressão:

∆ p = ρ Q w ln ⁡ r 2 r 1 2 r 2 2 - r 1 2 2 r 1 2 r 2 2

∆ p = ρ Q 2 r 2 2 - r 1 2 2 r 1 2 r 2 2 w 2 ln ⁡ r 2 r 1 2

Isolando Q na equação:

Q 2 = 2 r 1 2 r 2 2 w 2 ln ⁡ r 2 r 1 2 ∆ p ρ r 2 2 - r 1 2

Q = w ln ⁡ r 2 r 1 2 r 1 2 r 2 2 ∆ p ρ r 2 2 - r 1 2

Pelo enunciado:

k = w ln ⁡ r 2 r 1 2 r 2 2 r 1 2 ρ r 2 2 - r 1 2

Logo:

Q = k ∆ p

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Com suas próprias palavras, liste pelo menos três “alertas” para prestar atenção ao executar cálculos de camada limite laminar.
O ar flui paralelo a uma placa de limite de velocidade em uma rodovia à velocidade V = 5 m/s. A temperatura do ar é 25 °C e a largura W da placa paralela à direção do escoamento é 0,45 m. A camada lim
Com suas próprias palavras, faça um resumo dos cinco passos do procedimento da camada limite.
Ar a 30 °C flui a uma velocidade uniforme de 25,0 m/s ao longo de uma placa plana e lisa. Calcule a posição x aproximada ao longo da placa onde a camada limite começa o processo de transição para a tu
Considere duas tomadas de pressão ao longo da parede de uma camada limite laminar como na Figura P10-68. O fluido é o ar à temperatura de 25 °C, U 1 = 10,3m / s e a pressão estática P 1 é 2,44 Pa acim