Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 119

Repita o Problema 3-118 para uma altura de água de 1,2   m acima da dobradiça em B .

Passo 1

Temos um portão que está para ser aberto por uma força normal aplicada, temos que determinar a mínima força necessária para abrir.

Assumindo que a pressão atmosférica atua nos dois lados do portão, e devido a isto podemos ignora-la por convenção. Assumindo que o atrito na dobradiça será insignificante.

Tomaremos a densidade da água como padrão ρ w = 1000   k g / m 3 .

Para determinarmos a força mínima no centro do portão determinaremos o momento do portão.

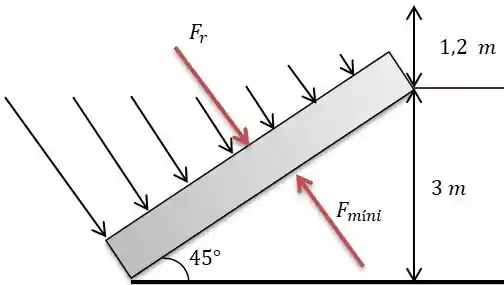
Passo 2

Bem vamos começar encontrando as coordenadas do centro do nosso portão, nosso portão configura um triangulo retângulo. Portanto, chamando a superfície que encontra na água do portão de b vamos calcular o comprimento de b e da superfície de água que não está na horizontal com o portão que chamaremos de s .

s e n   45 ° = 3 b

b = 3 s e n   45 ° ≅ 4,243   m

E

s e n   45 ° = 0,5 s

s = 1,2 s e n   45 ° = 1 , 697   m

Podemos determinara a força resultante no centro do portão pela pressão e a área. Como pressão é k g m ∙ s 2 e força [ k g   m / s 2 ] , basta multiplicarmos pela área m 2 e teremos a força.

F r = P ∙ A = ρ w g h c ∙ A

Em que h c começa na metade do portão até superfície da água, ou seja, 1,5 + 1 , 2 .

F r = 1000 ∙ 9,81 ∙ 2 , 7 ∙ 5 ∙ 4,243

F r = 5 6 2   k N

Passo 3

Agora para lidarmos com o momento no ponto B , vamos determinar a distância do centro da pressão até a superfície da água ao longo do plano do portão:

y p = s + b 2 + b 2 12 s + b 2

y p = 1,697 + 4,243 2 + 4,243 2 12 1,697 + 4,243 2 = 4 , 211   m

A distância do centro da pressão da roldana até o ponto B é:

L p = y p - s = 4,21 - 1,697 = 2 , 514   m

As distâncias necessárias calculadas, podemos determinar o momento no ponto B que é igual a zero e igual a nossa relação de momento e força média mínima:

∑ M B = 0

F r ∙ L p = F m í n i ∙ b 2

F m í n i = 2 F r ∙ L p b = 2 ∙ 562 ∙ 2 , 541 4,243 = 666   k N

Resposta

F m í n i = 666   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barragem de concreto (d = 2,5) é construída na forma de um triângulo isósceles, como na Figura P2.80. Analise essa geometria para encontrar o intervalo de ângulos θ para o qual a força hidrostátic
A barragem na Figura P2.82 é um quarto de círculo com largura de 50 m. Determine os componentes horizontal e vertical da força hidrostática contra a barragem e o ponto CP em que a resultante atinge a
A comporta AB na Figura P2.83 é um quarto de círculo de 3 m de largura, articulada em B. Encontre a força F suficiente apenas para impedir que a comporta se abra. A comporta é uniforme e pesa 13.350 N
Determine (a) a força hidrostática total sobre a superfície curva AB da Figura P2.84 e (b) sua linha de ação. Despreze a pressão atmosférica e considere a superfície com largura unitária.
A garrafa de champanhe (d = 0,96) da Figura P2.87 está sob pressão, como mostra a leitura do manômetro de mercúrio. Calcule a força líquida sobre a extremidade hemisférica de 50 mm de raio no fundo da