Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 80
Uma barragem de concreto (d = 2,5) é construída na forma de um triângulo isósceles, como na Figura P2.80. Analise essa geometria para encontrar o intervalo de ângulos para o qual a força hidrostática tenderá a virar a barragem no ponto B. A largura da barragem é b.
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
A primeira ideia que a gente tem que ter da questão é de qual assunto ela faz parte. Esse problema em específico é referente à seção 2.5 do livro, chamada “Forças sobre superfícies planas”.
Pra entender a questão, dá uma olhada no esquema abaixo.
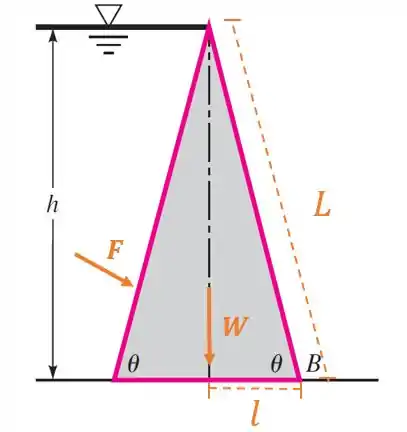
Algumas considerações devem ser feitas antes de começarmos a resolver a questão. Em primeiro lugar, temos duas forças agindo nessa barragem: a força hidrostática e a força peso da própria estrutura.
Além disso, o ângulo ao qual o enunciado se refere será como chamaremos o ângulo de inclinação da barragem, o comprimento do lado inclinado e a base da barragem.
A partir dessas considerações, iremos encontrar o intervalo de ângulos que fará a barrage virar no ponto .
Em primeiro lugar, devemos definir e a partir de simples relações trigonométricas ao olhar a figura. Sendo assim, temos que:
Da mesma fora, devemos também definir o braço de alavanca da força e da força . A primeira pode ser definida simplesmente como , ao olharmos a figura. Já a segunda, podemos definir também com base e relações geométricas como .
Por fim, devemos formular expressões para as forças envolvidas no problema.
Para a força :
Sendo o peso específico da água e o volume da água pra geometria da barragem, que é um triângulo retângulo. Portanto:
Já para a força :
Sendo a densidade do concreto e o volume da barragem.
Logo:
No próximo passo, iremos montar um balanço de momento e calcular o intervalo de ângulos .
Passo 2
Para resolver a questão, devemos montar um balanço de momento com relação a ponto . Temos, pela figura, que o momento causado pela força rotacionaria em um sentido horário, enquanto rotacionaria em um sentido anti-horário.
Desta forma, o balanço de momento é:
Nós queremos encontrar o ângulo crítico acima do qual a barragem irá se mover no ponto . Isso quer dizer que, para encontrar esse ângulo, os momentos precisa estar em equilíbrio e . Portanto, ficamos com a equação:
Resolvendo numericamente, temos que . Ou seja, para ângulos maiores que a força hidrostática tenderá a virar a barragem no ponto B
Resposta
Para , a força hidrostática tenderá a virar a barragem no ponto B.