Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 7.Problemas - Ex. 36

Repita o problema 7-35 considerando que o dissipador foi pintado de preto e , portanto, tenha emissivdade efetiva de 0,9. Note que nos cálculos de radiação, está sendo utilizada a superfície da base (10 cm x 6,2 cm) e não a superfície total.

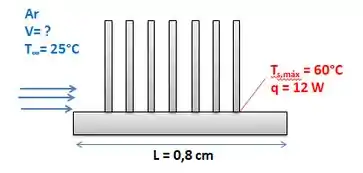
Passo 1

Esse problema só parece assustar, mas basicamente o que ele tá pedindo é pra gente fazer o raciocínio contrário do que estamos acostumados! Se liga só...

Ele pede a velocidade, certo? E dentro dos problemas de convecção, em qual variável a gente consegue ver a velocidade do fluido? Reynold

Agora vamos lá, Reynold está sempre relacionado com outro número adimensional que é Nusselt que por sua vez está relacionado com h.

Ok! Mas o que então a gente tem que fazer? Vou te passar um fluxograma rapidinho de como fica a ideia desse problema.

E n c o n t r a r   h → c a l c u l a r   N u → C a l c u l a r   R e → E n c o n t r a r   V

Mas antes, vamos pegar as propriedades do fluido em Tf = 42, 5°C

K = 0,027   W / m . K

v = 1,7   x   10 - 5   m ² / s

P r = 0,72 5

Passo 2

Aqui, é um pouquinho diferente a resolução em relação ao problema 7-35. Para este caso, precisamos lembrar que o calor que sai total do sólido para o ar está relacionado com a convecção (aleta ar) E radiação:

q t o t a l = q c o n v + q r a d

q c o n v = q t o t a l - q r a d

q c o n v = 12 - σ ε A b T s 4 - T ∞ 4

q c o n v = 12 - 5,67   x   10 - 8   x   0,9   x   0,062   x   0,1 x   60 + 273 4 - 25 + 273 4 = 10,6   W

Ou seja, temos que 10,6 W saem por convecção da aleta para o ar

Passo 3

Como a gente viu, o calor dissipado por convecção está associado a troca de calor entre aleta e fluido externo, então...

q c o n v = ɳ h A s T s - T ∞

h = q A s ɳ T s - T ∞

A s = A s u p e r f .   l a t e r a l   d a   a l e t a + A b a s e   n ã o   a l e t a d a

A s u p e r f .     l a t e r a l   d s   a l e t a = 2 L a l e t a x   H a l e t a   x   N a l e t a

A s u p e r f .   l a t e r a l   d a     a l e t a = 2   x   0,005   x   0,1   x   7 = 0,007   m ²

OBS: A gente despreza á área relacionada a Haleta x taleta, onde taleta = espessura, porque essa área vai ser muito menor quando comparada a área da superfície lateral

A b a s e   n ã o   a l e t a d a = A b a s e - N a l e t a A b a s e   d a   a l e t a

A b a s e   n ã o   a l e t a d a = 0,1   x   0,062 - 7   x   0,002   x   0,1 = 0,0048   m ²

Logo, A s = A s u p e r f .   l a t e r a l   d a   a l e t a + A b a s e   n ã o   a l e t a d a = 0,007 + 0,0048 = 0,0118   m ²

Agora é só substituir os valores das variáveis:

h = q A s ɳ T s - T ∞ = 10,6 0,0118   x   1   x   60 - 25 = 2 5 , 67 W m 2 ° C

Passo 4

Próximo passo é calcular Nusselt, se liga!

N u = h L K = 25 , 67   x   0,1 0,027 = 95,6

Agora vamos assumir que seja um escoamento laminar e usar a correlação para esse regime e considerando uma placa plana.

N u = 0,664   R e L 0,5 P r 1 3

R e L = N u 0,664   P r 1 3 2

Vamos abrir Reynold e isolar V

V L v = N u 0,664   P r 1 3 2 → V = v L N u 0,664   P r 1 3 2

V = 1 , 7   x   10 - 5 0,1 x   95,6 0,664   x   0,725 1 3 2 = 4,5   m / s

Essa resposta faz sentido, já que agora a gente tem um pouco de calor sendo perdido na forma de radiação, vamos precisar que saia menos por convecção, e portanto, vai exigir uma velocidade de escoamento menor.

Resposta

V = 4,5   m / s  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

84 - Repita o Prob.7-88 para arranjo escalonado com S L = S T = 6c m .
77 – Ar deve ser aquecido passando através de um banco de tubos de 3m de comprimento no interior onde ocorre condensação de vapor a 100℃ ℃. O ar aproxima-se do banco de tubos na direção normal a 20℃ ℃
80 – Água a 15℃ ℃ deve ser aquecida a 65℃ ℃ na passagem por um feixe de barras de resistência de aquecimento de 4m de comprimento e 1c m de diâmetro, mantidos a 90℃ ℃. A água aproxima-se do feixe de b
82- Repita o Prob. 7-81 resolvendo para um arranjo escalonado com S T = S L = 1,5c m e comparar o desempenho do evaporador para arranjos em linha e escalonado.
83 - O ar de combustão em uma instalação de fabricação deve ser pré-aquecido antes de entrar em um forno por água quente a 90℃ ℃ que flui através dos tubos de um banco de tubos localizado em um duto.O