Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 7.Problemas - Ex. 21
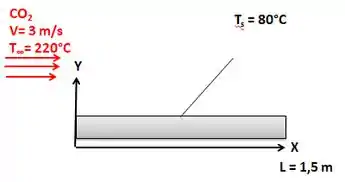
O dióxino de carbono quente dos gases de escapamento (a 1 atm) está sendo resfriado por meio de placas planas. O gás a 220°C está escoando paralelamente ao longo das superfícies superior e inferior de uma placa plana de 1,5 m de comprimento e uma velocidade de 3 m/s. Considerando que a temperatura da superfície plana da placa é mantida a 80°C. Determine (a) o coeficiente local de transferência de calor por convecção a 1 m a partir do bordo de ataque, (b) o coeficiente médio de transferência de calor por convecção sobre a placa inteira, e (c) o fluxo de transferência de calor total para a chapa.
Passo 1
(a) Como sempre, precisamos primeiro calcular o valor de reynold para entendermos como é o comportamento do fluido na posição desejada, que nesse caso é em X = 1
Vamos pegar as propriedades do CO2 na temperatura de filme e depois calcular reynold, belê?
Esse é um regime laminar porque estamos abaixo do reynold crítico para uma placa plana que é Re = 5 x 105, sacou?
Então agora é só usar a correlação apropriada às condições dadas e encontrar o valor de hX=1m, e a correlação para Nusselt local é:
Passo 2
(b) Para calcular o coeficiente de troca térmica convectivo médio, vamos seguir os passos idênticos feitos anteriormente, MASSSS a diferença é que agora queremos avaliar TODA A PLACA PLANA, então...
Ainda permanecemos num escoamento laminar, então vamos usar a mesma correlação que usamos para calcular h do problema anterior, certo?
NÃOOOOOOO!!!!
Queremos agora calcular o h médio e não mais o local, então indepente se o regime permaneceu laminar ou não, usamos outra correlação pois queremos outro parâmetro, beleza?
Passo 3
(c) Por fim, agora que temos o valor de h médio, podemos calcular o fluxo (W/m²) que é transmitido por convecção da seguinte maneira:
Obs: Não esquece de multiplicar a área por 2 porque estamos tendo troca de calor pela área inferior e superior da placa.