Os requisitos de ar comprimido de uma fábrica são atendidos por um compressor de que retira ar do exterior através de um duto com de comprimento e de diâmetro feito de folhas finas de ferro galvanizado. O compressor tira ar a uma taxa de às condições externas de e . Desprezando todas as perdas menores, determine a potência útil usada pelo compressor para superar as perdas por atrito nesse duto.
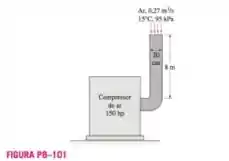
Passo 1
Bom gente, nesse problema temos que determinar a potência útil para superar as perdas por atrito. Primeiramente, potência útil é a potência da bomba, ou seja
Há outras expressões provenientes dessa acima. Para a diferença de pressão, usamos:
Mas para isso precisamos calcular o fator de atrito!
Passo 2
A partir de agora vamos calcular as variáveis que faltam! Show?? Como temos condições externas para e , os dados são , , . Então, para , temos:
Vamos começar pela rugosidade sobre o diâmetro :
Agora, calculamos a velocidade para conseguir o numero de Reynolds:
Assim, temos:
Passo 3
Tendo esses dados, vamos usar o diagrama de Moody para encontrar um valor para o fator de atrito:
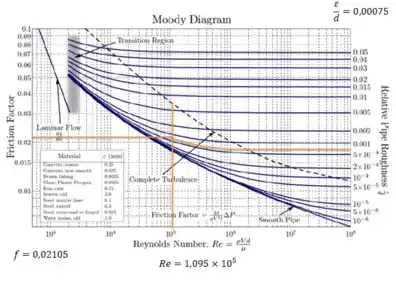
Assim, temos que . Portanto, substituindo na expressão do passo , temos:
Logo,
Prontinho!!