Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 8.Exercício - Ex. 7
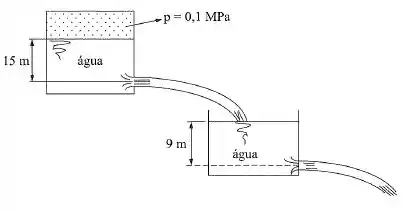
O reservatório superior descarrega a água, por um orifício cujo para um reservatório que, por sua vez, descarrega água por outro orifício. O sistema está em equilíbrio, de forma que o nível não muda em nenhum dos dois reservatórios. Qual será o coeficiente de descarga do segundo orifício? Dados: diâmetro do orifício (1): 9 cm; diâmetro do orifício (2): 10 cm.
Passo 1
Vamos começar aplicando o equilíbrio de energia para o reservatório superior:
Substituindo os valores conhecidos, temos:
Com a velocidade teórica em 1, podemos calcular a vazão teórica através de:
Substituindo os valores conhecidos:
Passo 2
Agora vamos usar o coeficiente de descarga do tanque 1 para descobrir a vazão real que sai desse reservatório:
Como o sistema opera em regime permanente, então a vazão real que sai de 1 e depois sai de 2 deve ser a mesma, então:
Passo 3
Agora, com o auxílio da equação 8.8 dessa seção, vamos encontrar a velocidade teórica na saída do reservatório 2:
Substituindo os valores conhecidos:
E, com isso, vamos calcular a vazão teórica no reservatório 2:
E, finalmente podemos encontrar o coeficiente de descarga do reservatório 2: