Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 18

As respostas aproximadas do Problema P7.11 são u =1,44 m/s e t = 0,0036 Pa em x = 50 cm e y = 5 mm (Não conte isso para seus colegas que estão trabalhando no Problema P7.11.) Repita este problema usando a solução exata de Blasius da camada-limite sobre uma placa plana.

Passo 1

E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!

Nessa questão, iremos refazer o problema 7.11, onde temos ar escoando a 20 ° C e 1   a t m escoando a 20 ° C sobre uma placa a uma velocidade U = 2   m / s .

A questão pede que a gente calcule a velocidade local u e a tensão cisalhante local τ na posição x , y = ( 50   c m , 5   m m ) utilizando a solução exata de Blausius, dada pela Equação (7.2) dada na página 471.

u U = f ' ( η )

η = y U ν x 1 / 2

Sendo ν = μ ρ   a viscosidade cinemática

Antes de ir pros próximos passos, vamos lembrar que a 20 ° C o ar tem massa específica ρ = 1,2   k g / m ³ e viscosidade μ =   1,8 × 10 - 5   P a ∙ s e, portanto, ν = 1,5 × 10 - 5   m 2 / s .

Agora vamo lá resolver essa questão juntos!

Passo 2

Em primeiro lugar, vamos resolver a letra (a) e encontrar a velocidade local u .

Primeiro, vamos calcular η :

η 50   c m , 5   m m = 0,005   m 2   m / s 1,5 × 10 - 5 m 2 s 0,5   m 1 / 2 ≈ 2,6

Agora, vãos calcular u / U utilizando a Tabela 7.1, dada na página 472. Vamos entrar com o valor de η e encontrar esse valor:

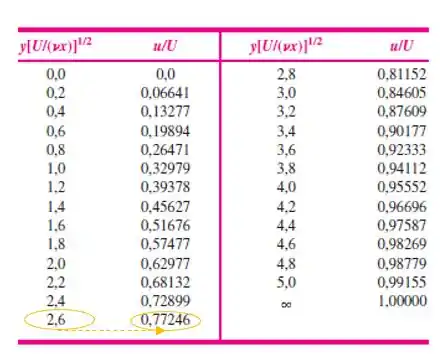
Portanto, u U = f ' η = 0,77246 .

Logo, a velocidade u é igual a:

u 2   m / s = 0,77246 → u = 1,54   m / s

Passo 3

Pra finalizar a questão, vamos resolver a letra (b) e calcular a tensão cisalhante local τ na posição   ( x ,   y ) .

τ = μ ∂ u ∂ y = μ ∂ ∂ y U f ' ( η ) = μ U U ν x 1 / 2 f ' ' ( η )

Nesse ponto, temos um problema: o livro não nos fornece ferramentas para calcular a segunda derivada de f ( η ) . Pra isso, precisamos ir no livro Mecânica dos Fluidos – Fundamentos e Aplicações, do Çengel.

Na página 456, temos a Tabela 10-3, encontramos a informação que a gente quer;

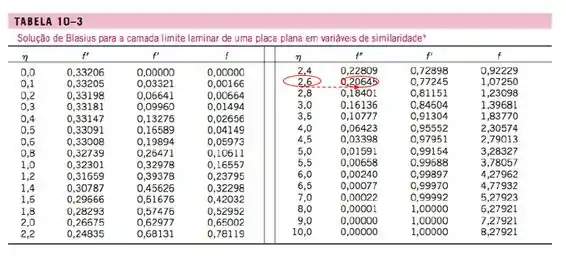
Por essa tabela, descobrimos que f ' ' η = 0,20645 .

Agora, podemos calcular τ :

τ = μ U U ν x 1 / 2 f ' ' η =   1,8 × 10 - 5   P a ∙ s 2   m / s 2   m / s 1,5 × 10 - 5 m 2 s 0,5   m 1 2 0,20645

τ = 0,0038   P a

Pronto, matamos a questão juntos!

Resposta

(a) A velocidade local é u 50   c m , 5   m m = 1,54   m / s

(b) A tensão cisalhante local é τ 50   c m , 5   m m = 0,0038   P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Problemas 9.18 e 9.19, o arrasto sobre a superfície superior da placa, para escoamento de corrente livre com U = 3m / s (massa específica do fluído ρ = 800k g / m 3 ), foi determinado para a placa
Considere um escoamento na camada limite laminar para estimar o arrasto sobre a placa plana mostrada quando colocada em um escoamento de ar a 5m / s . O ar está a 20 ° C e 101,3 k P a .
Usando os resultados numéricos obtidos por Blasius (Tabela 9.1), avalie a componente vertical de velocidade em uma camada limite sobre uma placa plana. Trace υ / U versus y / δ para R e x = 10 5 .
Consider turbulent fl ow past a sharp, smooth fl at plate ofwidth b and length L. What percentage of the friction dragon the plate is carried by the rear half of the plate?
Suppose you buy a 4- by 8-ft sheet of plywood and put iton your roof rack. (See Fig. P7.23.) You drive home at35 mi/h. (a) Assuming the board is perfectly alignedwith the airfl ow, how thick is the bo