Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 33

Usando os resultados numéricos obtidos por Blasius (Tabela 9.1), avalie a componente vertical de velocidade em uma camada limite sobre uma placa plana. Trace υ / U versus y / δ para R e x = 10 5 .

Passo 1

Queremos o gráfico de υ U versus y δ . Então o que precisamos fazer é encontrar uma relação matemática entre essas duas grandezas, através das equações de Blasius que a gente conhece. Vamos lá!

Passo 2

Podemos lembrar que por Blasius:

u = U f ' η ,     η = y   U ν x

Temos também a expressão da função corrente:

ψ = f η ν U x

A componente y da velocidade é definida por:

υ = - ∂ ψ ∂ x = - ∂ f η ν U x ∂ x

Temos que calcular essa derivada usando a regra da cadeia para f ( η ) e a regra do produto, pois há duas funções de x :

υ = - ∂ f ∂ x ν U x + ν U f η 2 ν U x

Passo 3

Calculando a derivada de f separadamente e jogando alguns termos para dentro da raiz:

∂ f ∂ x = ∂ f η ∂ x = ∂ f ∂ η ⋅ ∂ η ∂ x = f ' η - y 2 ⋅ 1 x U μ x

Lembrando que:  

    η = y   U ν x

∂ f ∂ x = f ' η - 1 2 x η

Voltando a expressão de υ :

υ = - f ' η - 1 2 x η ν U x + ν U f η 2 ν U x

Passo 4

Agora a gente só precisa arrumar esses termos, colocando o que der dentro das raízes:

υ = η 2 f ' η ν U x x 2 - 1 2 ν 2 U 2 ν U x f η = η 2 f ' η ν U x - 1 2 ν U x f η

Por fim,

υ = 1 2 ν U x η f ' η - f η

Passo 5

A gente pode dividir os dois lados por U e achar υ U :

υ U = 1 2 U ν U x η f ' ( η ) - f η

Jogando o U para dentro da raiz:

υ U = 1 2 ν U x U 2 η f ' ( η ) - f = 1 2 ν x U η f ' ( η ) - f η

Só que:

R e x = U x ν

Substituindo isso em   υ U :

υ U = η f ' η - f η 2 R e x

Passo 6

O enunciado disse que:

R e x = 10 5

Substituindo na nossa expressão:

υ U = η f ' η - f η 2 ⋅ 10 5 2

Podemos dizer que quando η = 5 , y = δ . Daí a gente pode usar essa relação:

y δ = 1 = η 5 ∴ y δ = η 5

Por fim, nossa relação entre υ U e y δ fica:

υ U = 5 y δ f ' 5 y δ - f 5 y δ 2 ⋅ 10 5 2

Passo 7

Para plotar o nosso gráfico a gente vai usar os resultados numéricos de Blasius aplicados a essa expressão:

υ U = η f ' η - f ( η ) 2 ⋅ 10 5 2

Fazendo isso, a gente tem esse gráfico:

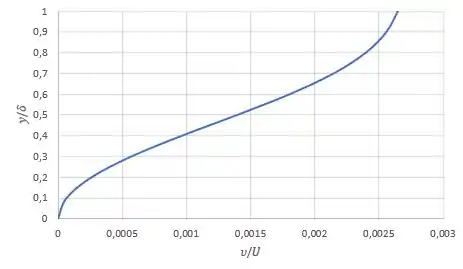
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resultados numéricos da solução de Blasius para as equações de Prandtl da camada limite são apresentados na Tabela 9.1. Considere o escoamento em regime permanente, incompressível, de ar-padrão sobre
Uma placa plana delgada é instalada em um túnel de água como uma divisora de fluxo. A placa tem 0,3m de comprimento e 1m de largura. A velocidade de corrente livre é 1,6m / s . Camadas limite laminare
Considere um escoamento na camada limite laminar para estimar o arrasto sobre a placa plana mostrada quando colocada em um escoamento de ar a 7 , 5m / s , porém considerando que a base da placa está d
Considere um escoamento na camada limite laminar para estimar o arrasto sobre a placa plana mostrada quando colocada em um escoamento de ar a 7 , 5m / s . O ar está a 20 ° C e a 101,3 k P a . (Note qu
Verifique que a componente y da velocidade para a solução de Blasius das equações da camada limite de Prandtl é dada pela Eq. 9.10. Obtenha uma expressão algébrica para a componente x da aceleração de