Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 149

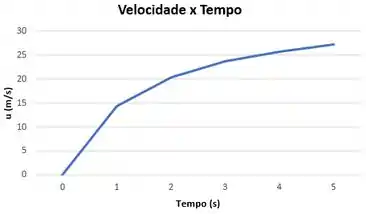
Partindo do repouso, o carrinho mostrado é propelido por uma catapulta hidráulica (jato de líquido). O jato atinge a superfície curva e é defletido de 180 ° , saindo na horizontal. As resistências de rolamento e do ar podem ser desprezadas. Se a massa do carrinho é de 100   k g e o jato de água sai do bocal (área 0,001   m 2 ) com uma velocidade de 35   m / s , determine a velocidade do carrinho 5   s após ser atingido pelo jato. Trace um gráfico da velocidade do carrinho em função do tempo.

Passo 1

Considerações Iniciais:

  1. Escoamento em estado estacionário;
  2. Escoamento incompressível;
  3. Escoamento com velocidade constante ( V = v - u ) ;
  4. Escoamento uniforme.
  5. Força de resistência desprezível.

Passo 2

Pelas considerações feitas no passo 1, utilizaremos a seguinte equação da quantidade de movimento:

F = F S + F B - ∫ V C a r ρ d ∀ = ∂ ∂ t ∫ V C V ρ   d ∀ + ∫ S C V ( ρ V ) d A = 0

Como estamos analisando um sistema x , temos:

F S x + F B x - ∫ V C a r f x ρ d ∀ = ∂ ∂ t ∫ V C u ρ   d ∀ + ∫ S C u ( ρ V ) d A

Não há forças de campo atuando no sistema e não a resistência, então, F B x = F S x = 0 :

- ∫ V C a r x ρ d ∀ = ∂ ∂ t ∫ V C u ρ   d ∀ + ∫ S C u ( ρ V ) d A

Não temos a variação das propriedades com o tempo, então:

∂ ∂ t = 0

Assim:

- ∫ V C a r x ρ d ∀ = ∫ S C u ( ρ V ) d A

Passo 3

- ∫ V C a r x ρ d ∀ = ∫ S C u ( ρ V ) d A

Para o fluxo de entrada, V   e   A possuem uma inclinação de 180°, então ρ V A = ( - ρ V A ) .

- a x ⋅ m = u 1 - ρ V A + u 2 ρ V A

u 1 = ( v - u ) ;

u 2 = - ( v - u ) .

Substituindo a x = d u d t :

- d u d t ⋅ m = v - u ⋅ - ρ ⋅ v - u ⋅ A - v - u ⋅ ρ ⋅ v - u ⋅ A

d u d t = 2 v - u 2 ⋅ ρ A m

d u v - u 2 = 2 ⋅ ρ A m d t

Substituindo d u por - d ( v - u ) :

- ∫ 0 u d ( v - u ) v - u 2 = ∫ 0 t 2 ⋅ ρ A m d t

∫ V v - u d ( v - u ) v - u 2 = ∫ 0 t 2 ⋅ ρ A m d t

Integrando, obtemos:

1 v - u - 1 v = 2 ⋅ ρ A m ⋅ t

Passo 4

Ajeitando a equação obtida:

v - ( v - u ) v ( v - u ) = 2 ⋅ ρ A m ⋅ t

Substituindo u = v - u :

v - u v ( v - u ) = u v ( v - u ) = 2 ⋅ ρ A m ⋅ t

Rearranjando:

v - u u = m 2 ρ A v t

v u - 1 = m 2 ρ A v t

v u = m 2 ρ A v t + 1

v u = m + 2 ρ A v t 2 ρ A v t

Finalmente, obtemos:

u = v ⋅ 2 ρ A v t m + 2 ρ A v t

Passo 5

Sendo:

v = 35   m / s ;

m = 100   k g ;

ρ = 1000   k g / m 3 ;

A = 0,001   m 2 ;

t = 5 s .

Temos:

u = 35 ⋅ 2 ⋅ 1000 ⋅ 0,001 ⋅ 35 ⋅ 5 100 + 2 ⋅ 1000 ⋅ 0,001 ⋅ 35 ⋅ 5 = 35 ⋅ 350 450 = 27,2   m / s  

Passo 6

Como:

u = 35 ⋅ 70 ⋅ t 100 + 70 ⋅ t

Traçaremos um gráfico da velocidade do carrinho em função do tempo.

Resposta

u = 27,2   m / s  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um veículo-foguete, pesando 44.500N e viajando a 960k m / h , deve ser freado pelo abaixamento de uma concha para dentro de um reservatório de água. A concha tem 150m m de largura. Determine o tempo n
Uma corrente de água, na condição-padrão, sai de um bocal de 50 mm de diâmetro e atinge uma pá curva, conforme mostrado. Um tubo de estagnação conectado a um manômetro de em tubo U com água e instalad
Um bocal plano descarrega verticalmente para baixo 1200 L/s por unidade de largura na atmosfera. O bocal é alimentado com um fluxo permanente de água. Uma placa plana estacionária, inclinada, colocada
Um medidor Venturi, instalado em uma tubulação de água, consiste em uma seção convergente, uma garganta de área constante e uma seção divergente. O diâmetro do tubo é D = 100m m e o diâmetro da gargan