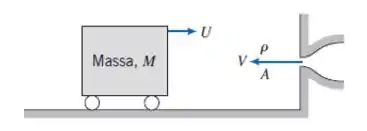
Um bloco retangular de massa , com faces verticais, rola sem resistência ao longo de um plano horizontal liso, conforme mostrado. O bloco viaja, inicialmente, à velocidade . Em , ele é atingido por um jato líquido e a sua velocidade começa a diminuir. Obtenha uma expressão algébrica para a aceleração do bloco para . Resolva a equação a fim de determinar o instante em que .

Pelas considerações feitas no passo 1, utilizaremos a seguinte equação da quantidade de movimento:

Como estamos analisando um sistema , temos:

Não há forças de campo atuando no sistema e não a resistência, então, :

Não temos a variação das propriedades com o tempo, então:

Assim:

Para o fluxo de entrada, possuem uma inclinação de 180°, então .

;

;

.

A expressão de aceleração se dá:

Substituindo :

Rearranjando:

Sendo :

Integrando:

Isolando :

Esse é o tempo necessário para ser igual a zero.