Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 123
Um revestimento superficial especial, sobre um painel quadrado com 5 m por 5 m de lado, é curado pela colocação do painel diretamente sob uma fonte de calor radiante que tem as mesmas dimensões. A fonte de calor é difusa e cinza, e opera com uma alimentação de potência de 75 kW. A superfície superior do aquecedor, bem como a superfície inferior do
painel, podem ser consideradas termicamente isoladas. O sistema encontra-se no interior de uma grande sala com ar e paredes a uma temperatura de 25°C. O revestimento superficial é difuso e cinza, com uma emissividade de 0,30 e um limite superior de temperatura de 400 K.
Desprezando os efeitos da convecção, qual é o espaçamento mínimo que pode ser mantido entre o aquecedor e o painel para assegurar que a temperatura do painel não ultrapasse 400 K? Levando em consideração os efeitos da convecção na superfície revestida do painel, qual deve ser o espaçamento mínimo?
Passo 1
Falaaaaaa galerinha !!
Vamos seguindo?
Bom, o problema nos pediu para achar duas coisas, não foi? A primeira é qual é o espaçamento mínimo que pode ser mantido entre o aquecedor e o painel para assegurar que a temperatura do painel não ultrapasse 400 K !!
Lembrando que neste caso não existe convecção:
O que nós sabemos é:
Para as radiosidades temos:
Lembrando que:
Substituindo:
Substituindo:
Bom, o fator de forma é que está relacionado ao distanciamento entre as placas, então precisamos acha-lo !!
Passo 2
Vamos começar achando o fator de forma em função do que queremos!
Pelo somatório para a superfície 1:
Por simetria:
Substituindo:
Abrindo a equação:
Só precisamos da emissividade então, não é?
Usando o calor que é transmitido através dos painéis 1 e 2:
Substituindo:
Substituindo na equação anterior:
Resolvendo:
Olhando na figura abaixo, quando e
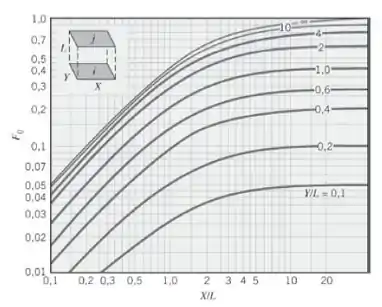
Assim nós obtemos:
Se
E assim nós achamos o espaçamento !!
Passo 3
A próxima pergunta da questão é o espaçamento mínimo, mas agora levando em consideração os efeitos da convecção na superfície revestida do painel!
Já sabemos que:
Isso não vai mudar, mas teremos uma nova radiosidade para a superfície 2. Agora quando fazemos o balanço energético para o painel 2:
Só precisamos do coeficiente convectivo, certo?
Antes de qualquer coisa precisamos calcular
Neste caso:
Para achar as propriedades do ar nós precisamos da temperatura média:
Assumindo que a temperatura seja próxima a e olhando na Tabela A – 4:
Substituindo:
E para o coeficiente:
Substituindo:
Agora vamos substituir, não é?
Passo 4
Agora que achamos o que precisávamos vamos colocar na equação do Passo 1:
Ainda precisamos de e para achar vamos fazer o balanço de energia para o painel 1:
Substituindo:
Resolvendo a equação:
Agora, quando olhamos no gráfico acima:
E é isso aí galerinhaa !!