Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 1.Problemas - Ex. 86
A right circular cylinder volume υ is to be calculated from
the measured base radius R and height H. If the uncertainty
in R is 2 percent and the uncertainty in H is 3 percent, estimate the overall uncertainty in the calculated volume.
Hint: Read Appendix E.
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
Os dados são os seguintes:
Volume do cilindro:
Raio do cilindro:
Altura do cilindro:
Incerteza no raio:
Incerteza na altura:
Passo 2
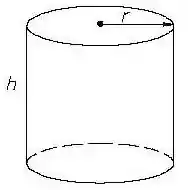
O volume do cilindro é
Volume é uma função de múltiplas variáveis:
A incerteza geral é calculada como
Onde
E
Passo 3
Então a incerteza geral é
Resposta
Exercícios de Livros Relacionados
O coeficiente de arrasto C A adimensional de uma esfera, a ser estudado nos Capítulos 5 e 7, é C A = F 1 2 ρ V 2 π 4 D 2 no qual F é a força de arrasto, ρ a massa específica do fluido, V é a velocidad
O Exemplo 1.10 fez uma análise que previa que em um disco em rotação, o momento viscoso M = π μ Ω R 4 2 h . Se a incerteza de cada uma das quatro variáveis ( μ ,Ω ,R ,h ) é 1%, qual é a incerteza tota
Duas placas paralelas. uma movendo-se a 4 m/s e a outra fixa, estão separadas por uma camada de 5 mm de espessura de óleo de densidade 0,80 e viscosidade cinemática 1,25 E-4 m 2 / s . Qual é a tensão
Um certo escoamento de água a 20 °C tem um número crítico de cavitação, onde se formam as bolhas, C a ≈ 0,25 , onde C a = 2 ( p a - p v a p ) / ρ V 2 . Se p a = 1a t m e a pressão de vapor é 0,34 libr
Se um corpo sólido uniforme pesa 50 N no ar e 30 N na água, sua densidade é1,5, (b) 1,67, (c) 2,5, (d) 3,0, (e) 5,0