Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 69
O que são equações constitutivas, e à que equação da mecânica dos fluidos elas são aplicadas?
Passo 1
Equações constitutivas são relações entre duas grandezas físicas que são específicas de materiais ou substâncias, quantificando respostas do material a estímulos externos. Podem ser expressas como proporcionalidades ou até mesmo como campos vetoriais ou tensoriais.
Para o caso específico da Mecânica dos Fluidos, equações constitutivas podem ser aplicadas na Equação de Cauchy, que trata da conservação do momento linear:
No nosso caso, as equações constitutivas vão nos ajudar a relacionar os componentes do tensor com a pressão e a velocidade do fluido.
Para isso, devemos lembrar como agem as forças superficiais num elemento diferencial de fluido a partir do esquema ilustrativo abaixo:
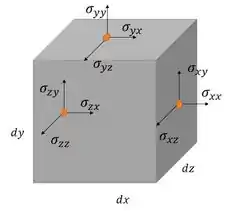
A partir dessa imagem, a gente pode separar as forças superficiais agindo no fluido em movimento como forças de pressão e tensões viscosas, a partir da equação:
Sendo a pressão e a tensão viscosa.
Nesse caso, já relacionamos o tensor com a pressão. Para relacionar com a velocidade, devemos lembrar da relação entre tensão de cisalhamento e velocidade a partir da seguinte equação constitutiva:
Sendo a viscosidade dinâmica do fluido e a taxa na qual a velocidade na direção varia na direção .
E é assim que as equações constitutivas podem ser aplicadas na Mecânica os Fluidos.
Resposta
Na Mecânica dos Fluidos, as equações constitutivas são relações entre o campo de tensores e o campo de pressões e de velocidade do problema, permitindo escrever a Equação de Cauchy em função da pressão e velocidade.