Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 1.Problemas - Ex. 52
Um secador de cabelos pode ser idealizado como um duto circular através do qual um pequeno ventilador sopra ar ambiente e dentro do qual o ar é aquecido ao escoar sobre uma resistência elétrica na forma de um fio helicoidal.
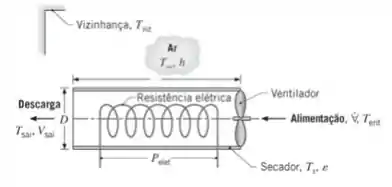
a) Se o aquecedor for projetado para operar com um consumo de potência elétrica e para aquecer o ar de uma temperatura ambiente até uma temperatura na saída de , em qual vazão volumétrica o ventilador deve operar? A perda de calor de seu revestimento externo para o ar ambiente e para a vizinhança pode ser desprezada. Se o duto tiver um diâmetro , qual é a velocidade do ar na saída ? A densidade do ar e o seu calor específico podem ser aproximados por e , respectivamente.
b) Considere um comprimento do duto do aquecedor e uma emissividade de sua superfície de . Se o coeficiente associado à transferência de calor por convecção natural do revestimento externo para o ar ambiente for de , e a temperatura do ar e da vizinhança for de , confirme que a perda de calor pelo revestimento externo é, de fato, desprezível. A temperatura superficial média do revestimento externo pode ser considerada igual a .
Passo 1
Letra a)
Para iniciarmos a resolução da questão temos que aplicar o princípio de conservação de energia ao sistema, onde a energia elétrica é usada para aquecer o ar:
Isolando a vazão mássica:
Sendo:
;
;
;
.
Temos:
Relacionando a vazão mássica com a massa específica, conseguimos obter a vazão volumétrica:
Sendo:
.
Temos:
Passo 2
Calculando a velocidade de saída:
Com:
.
Temos:
Passo 3
Letra b)
Aqui, temos que calcular a perda total de calor considerando a perda devido a convecção e radiação.
Dados:
;
;
;
;
;
;
.
Temos:
A quantidade é desprezível.