Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 15.Problemas - Ex. 33
Repita o Problema 15-31, exceto pela mudança das ventilações de fornecimento e/ou retomo do ar nas diversas localizações do teto. Compare e discuta.
Passo 1
Fala aí, galerinha. Tudo beleza? Vamos fazer mais uma questão de MecFlu pra tirar aquele na prova. Neste problema devemos gerar soluções CFD para várias resoluções de grade para testar a independência da grade para o fluxo através de um difusor. Especificamente, devemos comparar as linhas de fluxo e a diferença de pressão em cada nível de resolução da grade.
Neste caso, temos um escoamento incompressível, assimétrico em relação ao eixo e turbulento, mas constante na média. Dado que e .
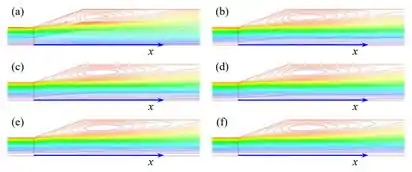
Na resolução de grade muito grosseira, as linhas de fluxo não são bem definidas. Podemos ver em :
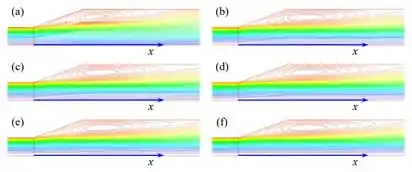
Sendo assim, o cálculo não é confiável. Conforme a resolução da grade melhora, os detalhes da região de separação do fluxo tornam-se mais refinados - a camada limite é incapaz de permanecer presa em um gradiente de pressão adverso tão forte.
A partir desses gráficos, parece que a independência da grade foi alcançada por volta do quarto caso , além do qual não há nenhuma mudança perceptível na forma das linhas de fluxo. Notamos que a simulação de separação de fluxo e bolhas de separação costuma ser uma tarefa muito difícil para um programa CFD. Neste problema específico, devemos usar uma grade extremamente fina a fim de resolver os detalhes da separação do fluxo.
Passo 2
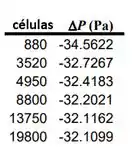
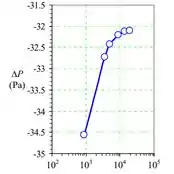
Por fim, temos que a variação de pressão é tabulado como uma função da contagem de células na tabela para o caso com . À medida que a resolução da grade melhora, ΔP aumenta e se torna independente da resolução da grade no quarta ou quinta malha. Isso também é visto na, onde é plotado como uma função da contagem de células. Fica assim:
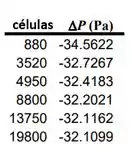
Plotando, temos:
É isso, galera. Bora pra praticar mais pra ficar craque.
Resposta
