Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 128

Silício sólido puro é produzido a partir de material fundido, como por exemplo, no Problema 1.42. Silício sólido é semitransparente e a distribuição do coeficiente de absorção espectral para o silício puro pode ser aproximada por:

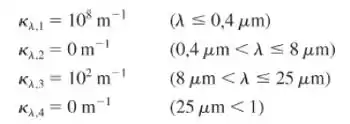
  1. Determine o coeficiente de absorção total, definido como:

κ = ∫ 0 ∞ κ λ G λ . d λ G

para a irradiação a partir da vizinhança a uma temperatura igual ao ponto de fusão do silício.

  1. Estime a transmissividade total, a absortividade total e a emissividade total de uma lâmina de silício sólido, com L = 150 μm de espessura, no seu ponto de fusão.

Passo 1

Animados para seguir que eu sei, não é?

Na letra (a) nós queremos achar o coeficiente de absorção total, ok?

O problema já nos deu a forma de calcular:

κ = ∫ 0 ∞ κ λ G λ . d λ G

Nós temos uma aproximação bastante utilizada por nós ao longo desde capítulo

κ ≈ ∫ 0 ∞ κ λ λ E λ , b λ . T f u s a o . d λ ∫ 0 ∞ E λ , b λ . T f u s a o . d λ

κ ≈ κ λ , 1 F 0 →   0,4 μ m . T f u s a o + κ λ , 2 F (   0,4 →   8 μ m . T f u s a o ) + κ λ , 3 F (   8 →   25 μ m . T f u s a o ) + κ λ , 4 F (   25 μ m . T f u s a o )

Sabendo que:

Então:

κ ≈ 10 8 F 0 →   0,4 μ m . T f u s a o + 10 2 F (   8 →   25 μ m . T f u s a o )

Para acha-lo nós precisamos lembrar que a temperatura de fusão do silício é 1685 K, e olhando a Tabela 12.2:

F 0 →   0,4   μ m × 1685   K = 0

F 0,4   μ m , 1685   K →   8   μ m , 1685   K = 0,955

F   8   μ m , 1685   K →   15   μ m , 1685   K = 0,998 - 0,955 = 0,043

F   15   μ m , 1685   K → ∞ = 1 - 0,998 = 0,0 02

Substituindo:

κ ≈ 10 8 0 + 10 2 0,04 3 = 4,3   m - 1

E assim nós chegamos ao fim da letra (a) !!

Passo 2

Na letra (b) nós queremos achar três coisas, a transmissividade total, a absortividade total e a emissividade total de uma lâmina de silício sólido, com L = 150 μm de espessura, na temperatura que já vimos, ok?

A transmissividade total é calculada usando a relação acima de forma adaptada:

τ = τ λ , 1 F 0 →   0,4 μ m . T f u s a o + τ λ , 2 F (   0,4 →   8 μ m . T f u s a o ) + τ λ , 3 F (   8 →   25 μ m . T f u s a o ) + τ λ , 4 F (   25 μ m . T f u s a o )

Os termos de F são os mesmos ! Mas os de τ λ nós conseguimos calcular por meio de uma fórmula bem tranquilinha:

τ λ = e - κ λ L

Substituindo os termos:

τ = e - 0 150 × 10 - 6 0,955 + e - 10 2 150 × 10 - 6 0,043 + e - 0 150 × 10 - 6 0,002

τ = 0,999

Nós ainda precisamos achar o valor da absortividade total!!

E esta aqui é bem legal, nós temos uma equação muito simplesinha:

α = 1 - τ = 1 - 0,999

α = 0,001

A relação entre emissividade e absortividade total é bem mais simples:

α = ε = 0,001

Molezinhaaa, né ?!

Que vocês acharam?

Resposta

  1. κ ≈ 4,3   m - 1
  2. τ = 0,999     |     α = ε = 0,001
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um forno tem a forma de uma seção de cone truncado, como mostrado na figura. O piso do forno tem uma emissividade de ε 1 = 0,7 e é mantido a 1000K com um fluxo térmico de 2200W / m 2 . A parede latera
Considere as cavidades formadas por um cone, um cilindro e uma esfera que têm o mesmo tamanho de abertura ( d ) e dimensão principal ( L ) , como mostrado na figura.(a) Determine o fator de forma entr
Um forno cúbico, com 2m de lado, é usado para tratar termicamente uma placa de aço. A superfície superior do forno é formada por aquecedores elétricos radiantes que têm uma emissividade de 0,85 e são
Silício sólido puro é produzido a partir de material fundido, como por exemplo, no Problema 1.37. Silício sólido é semitransparente e a distribuição do coeficiente de absorção espectral para o silício
Considere um forno circular que tem 0,5m de comprimento e 0,5m de diâmetro. As duas extremidades têm superfícies cinzas e difusas, que são mantidas a 400 e 500K , com emissividades de 0,4 e 0,5 , resp