Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 76

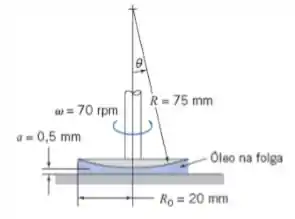
Uma seção reta de um mancal giratório é mostrada. O membro esférico gira com velocidade angular ω, a uma pequena distância, a, acima da superfície plana. A folga estreita é preenchida com óleo viscoso de viscosidade μ = 1250 cp. Obtenha uma expressão algébrica para a tensão de cisalhamento que atua no membro esférico. Avalie a tensão máxima de cisalhamento que atua sobre o membro esférico para as condições mostradas. (A tensão máxima está necessariamente localizada no raio máximo?) Desenvolva uma expressão algébrica (na forma de uma integral) para o torque de cisalhamento viscoso total que age no membro esférico. Calcule o torque utilizando as dimensões mostradas.

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Assumindo que o líquido em questão é newtoniano e que a velocidade é de perfil linear, temos que:

τ = μ d u d y

Já o torque, é dado por:

d T = r τ d A

Da figura, podemos tirar que:

r = R s e n θ

u = w r = w R s e n θ

d u d y = u - 0 h = u h

h = a + R ( 1 - cos ⁡ θ )

d A = 2 π R s e n θ R c o s θ d θ

Logo, teremos que:

τ = μ d u d y = μ w R s e n ( θ ) / ( a + R 1 - cos ⁡ θ

Para acharmos o máximo de uma função, devemos derivá-la e igualar a derivada a 0, logo:

τ ' = R μ w R c o s θ - R + acos ⁡ θ R + a - R c o s θ 2 = 0

R μ w R c o s θ - R + acos ⁡ θ = 0

Resolvendo a equação:

θ = 6,6 º

Logo, substituindo este valor na expressão da tensão, teremos:

τ = 79,2   N / m 2

Portanto, o torque será:

T = ∫ r τ A d θ = ∫ 0 θ m a x μ w R 4 s e n 2 θ ( a + R 1 - cos ⁡ θ d θ  

Onde:

θ m á x = a r c s e n R 0 R = 15,5

Logo, fazendo a integração e substituindo:

T = 1,02 × 10 - 3 N m

Resposta

T = 1,02 × 10 - 3 N m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Repita o Exemplo 1.12 fazendo os componentes da velocidade crescerem linearmente com o tempo: V = K x t i - K y t j + 0 k Calcule e esboce, para alguns tempos representativos, as linhas de corrente in
Para um viscosímetro de cone-placa da Figura P1.56, considere R = 6c m e θ = 3 ° . (a) Se o torque requerido para girar o cone a 600 rpm for 0,157 N.m, qual a viscosidade do fluido? (b) Se a incerteza
O coeficiente de arrasto C A adimensional de uma esfera, a ser estudado nos Capítulos 5 e 7, é C A = F 1 2 ρ V 2 π 4 D 2 no qual F é a força de arrasto, ρ a massa específica do fluido, V é a velocidad
O Exemplo 1.10 fez uma análise que previa que em um disco em rotação, o momento viscoso M = π μ Ω R 4 2 h . Se a incerteza de cada uma das quatro variáveis ( μ ,Ω ,R ,h ) é 1%, qual é a incerteza tota
Duas placas paralelas. uma movendo-se a 4 m/s e a outra fixa, estão separadas por uma camada de 5 mm de espessura de óleo de densidade 0,80 e viscosidade cinemática 1,25 E-4 m 2 / s . Qual é a tensão