Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 68

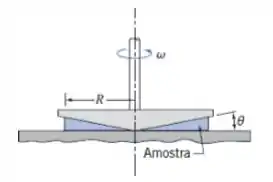
O viscosímetro do Problema 2.67 foi usado para medir a viscosidade aparente de um fluido. Os dados abaixo foram obtidos. Que tipo de fluido não newtoniano é este? Determine os valores para k e n usados nas Eqs. 2.16 e 2.17 de definição da viscosidade aparente de um fluido. (Considere θ igual a 0,5º.) Avalie a viscosidade a 90 e a 100 rpm.

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Sabemos que, para um raio qualquer, o gradiente de velocidade é:

d u d y = r w r t g θ

Onde w é a velocidade angular, dada por:

w = 2 π N 60

Como o ângulo θ é pequeno, podemos afirmar que t g θ = θ .

Logo:

d u d y = ω θ

Da equação 2.11:

k d u d y n - 1 d u d y = n d u d y

Onde n   é a viscosidade aparente.

Logo, a viscosidade aparente será:

n = k w θ n - 1  

Para os dados do problema:

  Teremos que:

Substituindo:

k = 0,0449

n = 1,21

Este fluido é dilatante.

Logo, para 90 e 100 rpm:

Resposta

Este fluido é dilatante.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Repita o Problema 1.83 para encontrar a equação e esboçara linha de trajetória que passa através de ( x 0 ,y 0 ) no instante t = 0 .
Um campo de velocidade não permanente bidimensional é dado por u =x ( 1 + 2 t ) , ν = y . Encontre a equação das linhas de corrente variáveis no tempo, que passam, todas, através do ponto ( x 0,y 0 )
Um campo de velocidade permanente bidimensional é dado por u = x 2 – y 2 ,ν = – 2 x y . Deduza o campo de linhas de corrente e esboce algumas linhas de corrente no semiplano superior.Dica: a equação d
Óleo, com uma pressão de vapor de 20k P a , é entregue por um oleoduto, com bombas igualmente espaçadas; cada uma delas aumenta a pressão do óleo em 1,3M P a . As perdas por atrito na tubulação são 15
Um campo de velocidade é dado por u = V cos ⁡ θ , ν = V sen ⁡ θ e w = 0 , em que V e θ são constantes. Deduza uma fórmula para as linhas de corrente desse escoamento.