Seja a adutora do Exemplo 5.6, que está enterrada em um solo inicialmente a 20°C, que é subitamente submetido a uma temperatura na superfície constante de — 15°C por 60 dias. Use uma rotina computacional para obter as soluções a seguir.

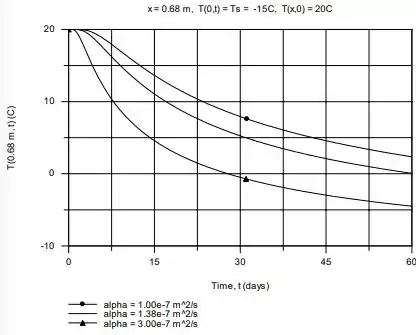
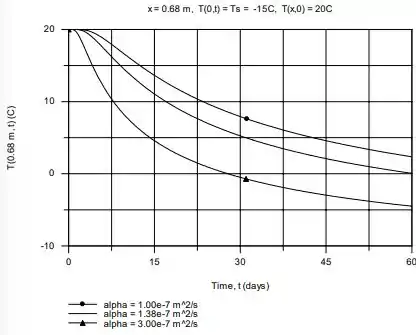
a) Calcule e represente graficamente o histórico da temperatura na profundidade de 0,68 m para difusividades térmicas de a X 107 = 1,0; 1,38 e 3,0 m2/s.

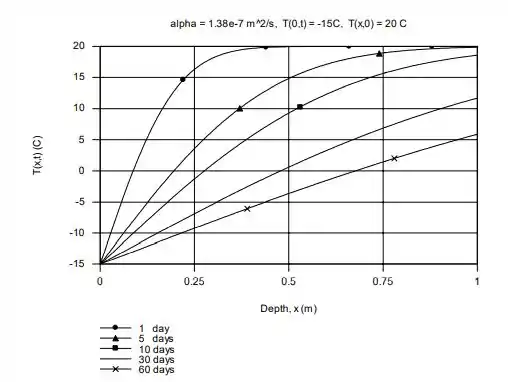
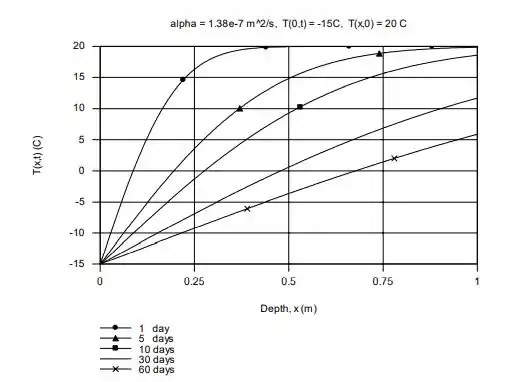
b) Para a = 1,38 X 10^7 m2/s, represente a distribuição de temperaturas na faixa de profundidades de 0 x 1,0 m para os tempos de 1, 5, 10, 30 e 60 dias.

c) Para a = 1,38 X 10^7 m2/s, represente a distribuição de temperaturas na faixa de profundidades de 0 x 1,0 m para os tempos de 1, 5, 10, 30 e 60 dias.

b) A distribuição de temperatura tempos selecionados pode ser vista no gráfico abaixo. Uma dica para vocês é compararem esse gráfico com o mostrado no Exemplo 5.6 do livro!

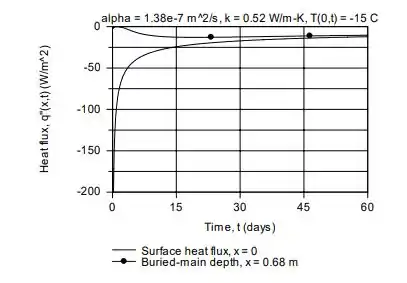
c) O fluxo de calor do solo , e o fluxo de calor à profundidade selecionada , são calculadas e plotadas para o período de tempo de .

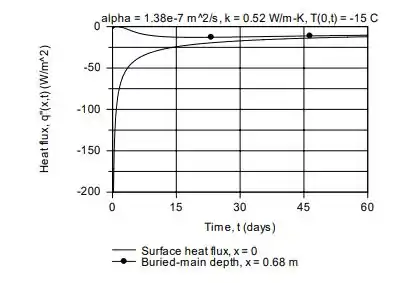
Uma coisa interessante é que ambos os fluxos de calor de superfície e subterrâneo têm um sinal negativo, pois o calor está fluindo no sentido negativo para a direção x. O fluxo de calor superficial é inicialmente muito grande e, no limite, aproxima-se do fluxo de calor principal enterrado. O último é inicialmente zero e, como o efeito da mudança repentina na superfície

temperatura é atrasada por um período de tempo, o fluxo de calor começa a aumentar lentamente.

Espero que tenham curtido! Nos vemos na próxima questão, galera!