Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 99
Seja a barreira de radiação cilíndrica do Exemplo , com de diâmetro, que está instalada concêntrica a um tubo transportando vapor de água com de diâmetro. A distância gera um espaço de ar com .
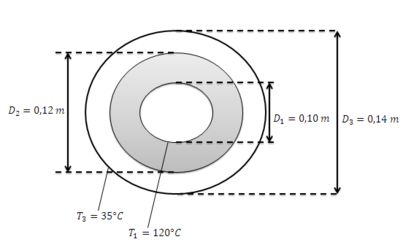
(a) Calcule a perda térmica por convecção, por unidade de comprimento do tubo, quando uma segunda barreira com de diâmetro é instalada e mantida a . Compare o resultado com aquele do exemplo para uma barreira.
(b) Na configuração com duas barreiras da parte (a), os espaços anulares de ar formados pelos tubos concêntricos têm . Calcule a perda térmica por unidade de comprimento do tubo se as dimensões dos espaços forem . Você espera que a perda térmica
aumente ou diminua?
Passo 1
Temos a seguinte situação: um tubo de água, de temperatura , é revestido com duas camadas de ar para diminuir as perdas de energia por convecção. Sabendo que a temperatura da camada externa é , devemos encontrar qual é a taxa de transferência de calor por comprimento do tubo e comparar este valor com o Exemplo , em que só havia uma camada de revestimento. Vamos lá?
A transferência de calor só ocorre por convecção. Além disso, vamos assumir que não ocorre acúmulo ou perda de energia no sistema. Então:
Precisaremos então calcular as condutividades efetivas de cada camada. Porém, as condutividades dependem da temperatura , que ainda não sabemos.
Para contornar isso, o que vamos fazer é estimar uma temperatura para e calcular as condutividades. Se escolhermos um valor adequado para então, o valor calculado por
E
Devem ser próximos e, pode-se dizer que correspondem à taxa de transferência de calor por unidade de comprimento de tubo.
Passo 2
Então, vamos começar estimando . O próximo passo é estimar a temperatura média do ar na primeira camada:
As propriedades do ar nesta temperatura são (Tabela A-4, apêndice A):
Vamos agora calcular o comprimento característico da primeira camada:
Agora que temos o comprimento característico podemos calcular o número de Rayleigh para esta camada:
O próximo passo para obter a condutividade térmica efetiva da primeira camada será aplicar a relação:
Podemos agora calcular a taxa de transferência de calor por convecção natural:
Passo 3
Iremos agora calcular a taxa de transferência de calor usando os dados da segunda camada de ar. Para começar, vamos calcular a temperatura média:
As propriedades do ar nesta temperatura são (Tabela A-4, apêndice A):
Vamos agora calcular o comprimento característico para a segunda camada:
Agora que temos o comprimento característico podemos calcular o número de Rayleigh para esta camada:
O próximo passo para obter a condutividade térmica efetiva será aplicar a equação:
A taxa de transferência de calor por convecção natural na segunda camada é:
Como os valores encontrados foram próximos vamos assumir que a temperatura é aproximadamente . Então, a taxa de transferência de calor por unidade de comprimento de tubo é um valor médio, em torno de .
Como podemos ver, este valor é menor que o encontrado no exemplo , . Isto ocorre porque a adição de uma nova camada de ar causa uma nova resistência térmica e isso diminui a taxa de transferência de calor.
Passo 4
Vamos agora para o item (b). Agora as espessuras das camadas de ar são ao invés de . Então, os novos diâmetros são e . Vamos seguir um procedimento similar ao que fizemos no item (a).
O primeiro passo é estimar a temperatura . Vamos dizer que , então, também teremos e .
Nosso próximo passo é determinar o novo comprimento característico da primeira camada:
Agora que temos o comprimento característico iremos calcular o número de Rayleigh:
O próximo passo será obter a condutividade térmica efetiva da primeira camada:
Podemos agora calcular a taxa de transferência de calor por convecção natural:
Passo 5
Vamos agora calcular a taxa de transferência de calor usando os dados da segunda camada. Começando pelo comprimento característico:
Nosso próximo passo é obter o número de Rayleigh:
Vamos agora para a condutividade térmica efetiva:
A taxa de transferência de calor por convecção natural na segunda camada é:
A taxa de transferência de calor médio neste caso é . Como podemos ver, houve um pequeno aumento no valor da taxa de transferência quando se aumenta a espessura das camadas de ar. Isto ocorre porque o aumento da espessura gera uma elevação da área de troca térmica, elevando a taxa de transferência.
Resposta
(a) ; este valor é menor que o encontrado no exemplo , . Isto ocorre porque a adição de uma nova camada de ar causa uma nova resistência térmica e isso diminui a taxa de transferência de calor.
(b) .