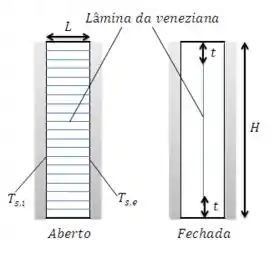
Considere uma veneziana que é instalada no espaço de ar entre as duas lâminas de uma janela vertical de vidro duplo. A janela tem de altura e de largura, e a veneziana tem lâminas que têm, cada uma, largura de . Quando a veneziana está aberta, espaços menores de seção quadrada são formados ao longo da altura da janela. Na posição fechada, a veneziana forma uma folha praticamente contínua com dois espaços abertos com no topo e na base do espaço entre os vidros da janela. Determine a taxa de transferência de calor por convecção entre a lâmina de vidro interna, que é mantida a , e a lâmina externa, que está a , estando a veneziana na posição aberta e na posição fechada, respectivamente. Explique por que a veneziana fechada tem pouca influência na transferência de calor por convecção através da cavidade.

Agora que temos as propriedades podemos seguir para o cálculo dos coeficientes convectivos. Vamos começar com a situação em que a veneziana está aberta. Neste caso, teremos espaços confinados quadrados, de lado . Para este caso o número de Rayleigh será:

Para escolher a correlação de Nusselt mais adequada devemos calcular a razão:

E

Para estes valores que encontramos a correlação mais adequada é:

Então, a taxa de transferência de calor é:

Vamos agora calcular a taxa de transferência de calor para a veneziana fechada. Para este caso, o número de Rayleigh se mantém. O que muda é a razão , que agora será:

Então, para esta nova razão a correlação de Nusselt mais adequada é:

E a taxa de transferência de calor para a veneziana fechada é:

Por fim, vamos justificar porque a presença da veneziana fechada têm pouca influência na troca térmica por convecção. Isto ocorre porque o movimento típico das correntes de convecção é similar à:

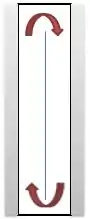
Ou seja, é comum na convecção natural que a massa de ar no centro do espaço esteja estagnada. Assim, a presença da veneziana não interfere nas correntes naturais de convecção e, por isso, têm pouca influência na taxa de transferência de calor.