Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 96

Seja o Problema 6.17. A placa estacionária, o ar ambiente e a vizinhança estão a T ∞ = v i z   =   20 ° C . Sendo a temperatura do disco em rotação de T s = 80 ° C , qual é a potência total dissipada a partir da superfície superior do disco para g = 2 mm, Ω = 150 rad/s, estando a placa estacionária e o disco pintados com tinta preta Parsons? Com o passar do tempo, a tinta sobre o disco em rotação se desgasta, expondo sua base metálica, que tem uma emissividade de ε = 0,10. Determine a potência total dissipada a partir da superfície superior do disco desgastada.

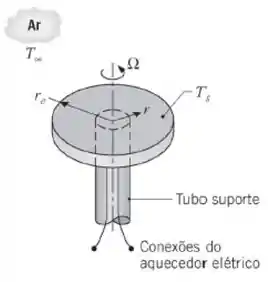
Passo 1

Vamos continuando?

Vamos dar uma ampliada neste desenho e ver de perto cada coisa:

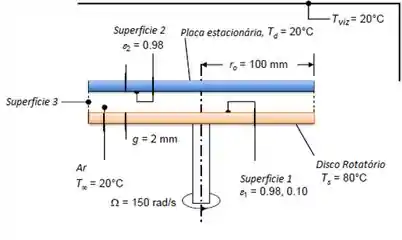
Bom galerinha, primeiro nós vamos avaliar a potência dissipada pela superfície superior da placa estacionária, que dissipa calor por convecção e a proveniente do disco rotativo:

q = q c o n v + q 1 , r a d

Nós teremos dois casos, mas no primeiro ε 2 = 0,98 . Vamos reescrever assim:

q = q c o n v + q 1 , r a d ,   0,98

Sabemos que:

q c o n v = h - A T s - T d

Sabemos que:

T s = 80 ° C

T d = 20 ° C

A = π r 0 2 = π 0,1 m 2

Lá do problema 6.17 temos que:

h ( r ) = k 70 1 + e - 140 G Ω r 0 2 v - 0,456 Ω v 0,478 r - 0,044

Para o coeficiente médio

h - = 1 A ∫ 0 r o h r . d A

h - = k π r 0 2 70 1 + e - 140 G Ω r 0 2 v - 0,456 Ω v 0,478 ∫ 0 r o r - 0,044 2 π r . d r .

h - = 2 π k π r 0 2 70 1 + e - 140 G Ω r 0 2 v - 0,456 Ω v 0,478 ∫ 0 r o r 0,956 d r

h - = 1,022 k r 0 2 70 1 + e - 140 G Ω r 0 2 v - 0,456 Ω v 0,478 r o 1,956

Sabemos que:

G = g r o = 0,002   m 0,1   m = 0,02

Ω   =   150 r a d s

Ainda precisamos das propriedades do ar, mas para isso vamos precisar achar a temperatura média:

T m e d i a = T s + T ∞ 2 = 80 ° C + 20 ° C 2 = 50 ° C + 273 = 323   K

Olhando na tabela A – 4 e interpolando:

k = 0,28 W m K

v = 18,20 × 10 - 6 m 2 s

Substituindo tudo:

h - = 1,022 0,28 W m K 0,1   m 2 70 1 + e - 140 0,02 150 r a d s 0,1   m 2 18,20 × 10 - 6 m 2 s - 0,456 150 r a d s 18,20 × 10 - 6 m 2 s 0,478 0,1   m 1,956

h - = 27,26 W m 2 K

Calculando o calor convectivo:

q c o n v = 27,26 W m 2 K π 0,1 m 2 80 ° C - 20 ° C

q c o n v = 51,38   W

Já achamos o calor convectivo agora vamos para o próximo?

Passo 2

Agora, para a taxa de transferência de calor removida do topo da pastilha nós usamos aquela fórmula que já até decoramos:

q i = E b i - J i 1 - ε i ε i A i = ∑ j = 1 3 J i - J j 1 A i F i j

Onde E b i é a potência emissiva, J i a radiosidade, A i a área e ε i a emissividade da superfície i.

Vamos dar uma olhada na equação aberta?

q 1 = E b 1 - J 1 1 - ε 1 ε 1 A 1 = J 1 - J 2 1 A 1 F 12 + J 1 - J 3 1 A 1 F 13

q 2 = E b 2 - J 2 1 - ε 2 ε 2 A 2 = J 2 - J 1 1 A 2 F 21 + J 2 - J 3 1 A 2 F 23

Nós sabemos que:

A = π 0,1 m 2 = 0,0314   m 2

Para calcular as potências emissivas:

E b 1 = σ T 1 4

E b 2 = σ T 2 4

E para a superfície 3:

E b 3 = J 3 = σ T 3 4

Lembrando que:

σ = 5,67 × 10 - 8   W m 2 K 4

T 1 = 80 ° C + 273 = 353   K

T 2 = 20 ° C + 273 = 293   K

T 3 = 20 ° C + 273 = 293   K K

Então:

E b 1 = 5,67 × 10 - 8   W m 2 K 4 353   K 4 = 880,40   W m 2

E b 2 = 5,67 × 10 - 8   W m 2 K 4 293   K 4 = 417,88   W m 2

J 3 = 5,67 × 10 - 8   W m 2 K 4 293   K 4 = 417,88   W m 2

Então nós só precisamos dos fatores de forma!!

Passo 3

Para discos paralelos coaxiais nós podemos usar a relação disposta na Tabela 13.2:

F 12 = 0,5   S - S 2 - 4 r 2 r 1 2 1 2

Lembrando que:

S = 1 + 1 + R 2 2 R 1 2

R 1 = r 1 g = 100   m m 2   m m = 50

R 4 = r 2 g = 100   m m 2   m m = 50

Então:

S = 1 + 1 + 50 2 50 2 = 2,0004

Colocando no fator de forma:

F 12 = 0,5   2,0004 - 2,0004 2 - 4 1 2 1 2 = 0,9802

Pela reciprocidade:

F 12 = F 2 1 = 0,9802

Fazendo o somatório para a superfície 1:

F 12 + F 13 = 1

F 13 = 0,0198

E para a superfície 2:

F 2 3 = 0,0198

Substituindo:

880,4 - J 1 1 - 0,98 0,98 × 0,0314   m 2 = J 1 - J 2 1 0,9802 × 0,0314   m 2 + J 1 - 417,88 1 0,0198 × 0,0314   m 2

417,88 - J 1 1 - 0,98 0,98 × 0,0314   m 2 = J 1 - J 2 1 0,9802 × 0,0314   m 2 + J 1 - 417,88 1 0,0198 × 0,0314   m 2

Resolvendo as duas equações simultaneamente:

J 1 = 871,3 W m 2

J 2 = 426,8 W m 2

E o calor deixando a superfície 1:

q 1 , r a d ,   0,98 = 880,4 - 871,3 1 - 0,98 0,98 × 0,0314   = 13,97   W

Vamos calcular o total?

q = 51,38   W + 13,97   W = 65,35   W

Passo 4

Bom, ainda não acabamos ! Precisamos saber da troca quando a rotação se desgasta, ou seja, ε   =   0,10 .

O calor convectivo não vai mudar, mas agora o calor devido a rotação será:

880,4 - J 1 1 - 0 , 10 0 , 10 × 0,0314   m 2 = J 1 - J 2 1 0,9802 × 0,0314   m 2 + J 1 - 417,88 1 0,0198 × 0,0314   m 2

417,88 - J 1 1 - 0,10 0,10 × 0,0314   m 2 = J 1 - J 2 1 0,9802 × 0,0314   m 2 + J 1 - 417,88 1 0,0198 × 0,0314   m 2

Resolvendo:

J 1 = 464,9 W m 2

J 2 = 417,9 W m 2

E o calor deixando a superfície 1:

q 1 , r a d ,   0,10 = 880,4 - 464,9 1 - 0,10 0 , 10 × 0,0314   = 1,45   W

Vamos calcular o total?

q = 51,38   W + 1,45   W = 52,83   W

Ufaa !! Acabamos mais umaa !!

Resposta

  1. 65,35   W
  2. 52,83   W
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A maioria dos arquitetos sabe que o teto de uma pista de patinação no gelo tem que ter uma alta refletividade. Caso contrário pode ocorrer condensação no teto e a água pingar sobre o gelo, causando ca
Considere duas placas paralelas muito grandes. A placa inferior é mais quente do que a superior, que é mantida a uma temperatura constante de T 1 =330K . As placas estão separadas por L = 0,1 m e no e
Discos metálicos revestidos são curados colocando-os na parte superior de um forno cilíndrico cuja superfície inferior (base) é eletricamente aquecida e cuja parede lateral pode ser aproximada por uma
Tubos de caldeiras expostos aos produtos da combustão de carvão em usinas de potência estão sujeitos à deposição de cinzas (minerais) presentes no gás de combustão. As cinzas formam um depósito sólido
Uma janela de vidro duplo tem duas placas de vidro, cada uma com espessura t = 6 mm. A temperatura no lado interior é T i=20 ° C , com h i =7,7 W m 2 K , enquanto a temperatura no lado externo é T e =