Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 97
A maioria dos arquitetos sabe que o teto de uma pista de patinação no gelo tem que ter uma alta refletividade. Caso contrário pode ocorrer condensação no teto e a água pingar sobre o gelo, causando calombos na superfície de patinação. A condensação irá ocorrer no teto quando sua temperatura superficial ficar inferior ao ponto de orvalho do ar ambiente
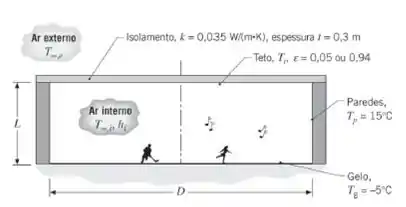
interno. Seu trabalho é efetuar uma análise para determinar o efeito da emissividade do teto na sua temperatura e, consequentemente, na propensão para haver condensação. A pista tem um diâmetro D = 50 m e a altura do ambiente interno é de L = 10 m, e as temperaturas do gelo e das paredes são –5°C e 15°C, respectivamente. A temperatura do ar interno é de 15°C e um coeficiente convectivo de caracteriza as condições na superfície do teto. A espessura e a condutividade térmica do isolamento do teto são 0,3 m e , respectivamente, e a temperatura do ar externo é de – 5°C. Considere que o teto é uma superfície difusa e cinza e que as paredes e o gelo podem ser aproximados por corpos negros.
- Considere um teto plano com uma emissividade de 0,05 (painéis altamente refletivos) ou de 0,94 (painéis pintados). Efetue um balanço térmico no teto para calcular os valores correspondentes da temperatura do teto. Se a umidade relativa do ar interno é de 70%, ocorrerá condensação para uma ou para as duas emissividades?
- Para cada uma das emissividades, calcule e represente graficamente a temperatura do teto como uma função da espessura do isolante para 0,1 ≤ t ≤ 1 m. Identifique condições nas quais a condensação irá ocorrer no teto.
Passo 1
Vamos que vamos galerinha ?!
A letra (a) nos pede para calcular a temperatura do teto para dois casos: e
é relativamente simples, nos pede para representar os processos térmicos relevantes para a pastilha, tranquilo?
Primeiro nós faremos o balanço de energia para o teto:
No caso do teto nós não temos nenhuma transferência de calor sendo adicionada, só temos calor saindo por condução, convecção e radiação:
Vamos lembrar como se calcula cada uma, mas vamos começar pela condução:
Lembrando que:
Então:
A convectiva também nós estamos carecas de saber, não ?
E aqui nós temos é:
Substituindo:
Passo 2
Para a radioativa nós vamos usar uma relação nova:
Como o teto é uma superfície difusa e cinza:
Vamos calcular as áreas que ainda não temos?
Para as potências emissivas nós sabemos que:
Lembrando que:
Ao invés de calcular de uma vez, vamos colocar na fórmula, ok?
Então nós só precisamos dos fatores de forma!!
Para discos paralelos coaxiais, como a pastilha e a grade nós podemos usar a figura abaixo:
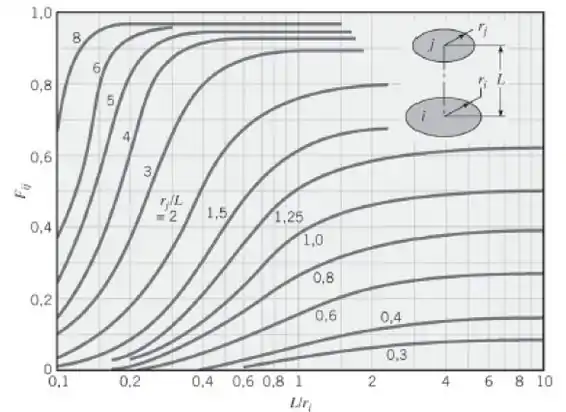
Se:
Fazendo a razão:
Olhando no gráfico:
Fazendo o somatório para a pastilha:
Pela reciprocidade:
Agora temos tudo o que precisamos certo?
Passo 3
Quando
Colocando no balanço de energia:
Resolvendo:
Em graus Celsius:
Quando
Colocando no balanço de energia:
Resolvendo:
Em graus Celsius:
Uma coisa muito importante galera, quando nós temos uma umidade relativa de 70% e a temperatura de bulbo seco igual a temperatura interna, 15°C, podemos obter na carta psicométrica e achar que a temperatura do ponto de orvalho é:
Ou seja:
Como a temperatura para é maior do que a de orvalho, não haverá condensação. Já para haverá !!
Terminamos a letra (a) mais temos a letra (b) !!
Passo 4
Para a letra (b) queremos, dadas as mesmas emissividades, queremos calcular e representar graficamente a temperatura do teto como uma função da espessura do isolante para 0,1 ≤ t ≤ 1 m.
Quando nós variamos a espessura nós variamos apenas o calor por condução, certo?
Então nós teremos que calcular o calor condutivo no Passo 1 e assim repetir o Passo 4!!
Vamos usar um software para facilitar e obter:
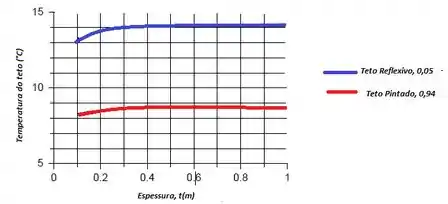
Legal, não foi ?!
