Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 98

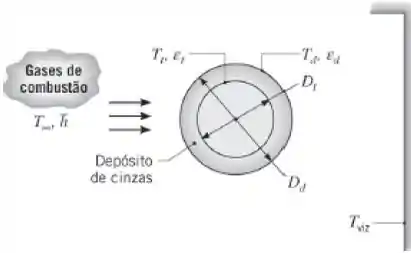
Tubos de caldeiras expostos aos produtos da combustão de carvão em usinas de potência estão sujeitos à deposição de cinzas (minerais) presentes no gás de combustão. As cinzas formam um depósito sólido sobre a superfície externa dos tubos, que reduz a transferência de calor para uma mistura pressurizada de água e vapor que escoa no interior dos tubos. Considere um tubo de caldeira com parede delgada ( D t   =   0,05   m ) , cuja superfície é mantida a T t =   600   K pelo processo de ebulição. Os gases de combustão, escoando sobre o tubo a T ∞ =   1800   K , proporcionam um coeficiente convectivo de h - = 100 W m 2 K , enquanto a radiação

incidente no tubo a partir do gás e das paredes da caldeira pode ser aproximada por aquela que se origina de uma grande vizinhança a T v i z =   1500   K .

  1. Se a superfície do tubo é difusa e cinza, com ε t   =   0,8 , e não existe a camada de depósito, qual é a taxa de transferência de calor por unidade de comprimento, q′, para o tubo da caldeira?
  2. Se uma camada de depósito, com diâmetro D d =   0,06   m e condutividade térmica k = 1 W m K , se formar sobre o tubo, qual é a temperatura da superfície do depósito, T d ? O depósito é difuso e cinza, com ε d   =   0,9 . Os valores de T t , T ∞ , e T v i z permanecem sem alteração. Qual é a taxa líquida de transferência de calor por unidade de comprimento, q′, para o tubo da caldeira?
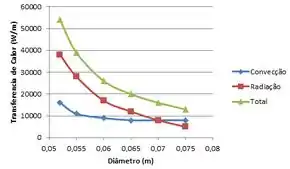
  3. Explore o efeito de variações em D d e sobre q′, assim como sobre as contribuições relativas da convecção e da radiação para a taxa de transferência de calor líquida. Represente graficamente os seus resultados.

Passo 1

Falaaaa galerinha !! Como vocês estão !!

Espero que firmes e fortes ! hashas

Bom, a letra (a) nos pede para encontrar a taxa de transferência de calor por unidade de comprimento, q′, para o tubo da caldeira, sabendo que ε t   =   0,8 , e não existe a camada de depósito, tranquilo?

Se não há depósito a transferência de calor ocorre por convecção e radiação:

q ' = q ' c o n v + q ' r a d

Sabemos que:

q ' c o n v = h - A T ∞ - T t

q ' r a d = ε t σ A T v i z 4 - T t 4

Então:

q ' = h - A T ∞ - T t + ε t σ A T v i z 4 - T t 4

Sabendo que:

h - = 100 W m 2 K

σ = 5,67 × 10 - 8   W m 2 K 4

T ∞ = 1800   K

T t = 600   K

T v i z = 1500   K

A = π D t = π 0,05   m

Então:

q ' = 100 W m 2 K π 0,05   m 1800   K - 600   K + 0,8 5,67 × 10 - 8   W m 2 K 4 π 0,05   m 1500 4 - 600 4 K 4

q ' = 53997,12 W m  

Terminamos a letra (a) e já seguimos para a (b)!!

Passo 2

Na letra (b) queremos a taxa de transferência de calor quando há a camada de depósito. Quando acontece isso nós temos as duas transferências de calor que ele está recebendo sendo transferida por condução para a superfície:

q ' c o n v + q ' r a d = q ' c o n v

Neste caso, as novas taxas levam em consideração a temperatura deste depósito:

q ' c o n v = h - π D d T ∞ - T d

q ' r a d = ε t σ π D d T v i z 4 - T d 4

q ' c o n d = 2 π k T d - T t ln ⁡ D d D t

Então:

2 π k T d - T t ln ⁡ D d D t = h - π D d T ∞ - T d + ε t σ π D d T v i z 4 - T d 4

Sabendo que:

D d =   0,06   m

k = 1 W m K

ε d   =   0,9

Podemos só substituir:

2 π 1 W m K T d - 600   K ln ⁡ 0,06   m 0,05 = 100 W m 2 K π 0,06   m 1800   K - T d + 0,9 5,67 × 10 - 8   W m 2 K 4 π 0,06   m 1500 4 - T d 4

Resolvendo:

T d = 1345,77   K

E para a taxa de calor, fazemos igual no passo 1:

q ' = 100 W m 2 K π 0,06   m 1800   K - 1345,77   K + 0,9 5,67 × 10 - 8   W m 2 K 4 π 0,06   m 1500 4 - 1345,77 4 K 4  

q ' = 25700 W m

Preparados para a letra (c)?

Passo 3

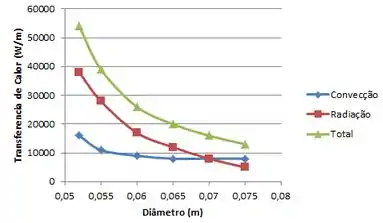
Na letra (c) nós queremos fazer um gráfico correlacionando as variações de D d sobre q′, assim como sobre as contribuições relativas da convecção e da radiação, ou seja, faremos o Passo 2 novamente !!

Se:

0,05 m ≤ D d ≤ 0,075   m

Utilizando um software nós obtemos:

Ufaa !! Acabamos mais umaa !!

Resposta

  1. q ' = 53997,12 W m
  2. T d = 1345,77   K   |   q ' = 25700 W m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o tubo e a barreira de radiação do Problema 13.49, mas agora leve em consideração a convecção natural no espaço entre o tubo e a barreira, assim como o fato de que a temperatura da barreira
A superfície de uma barreira de radiação voltada para uma parede negra quente, a 400 K, tem uma refletividade de 0,95. Fixada ao lado de trás da barreira há uma folha de material isolante com 25 mm de
O lado inferior de um disco com 400 mm de diâmetro é aquecido por um forno elétrico, enquanto o lado superior está exposto ao ar ambiente quiescente e a uma vizinhança, ambos a 300 K. O forno radiante
O tubo de chama de um sistema de aquecimento de água é constituído por um longo duto circular com diâmetro D = 0,07 m e temperatura Ts = 385 K, através do qual gases de combustão escoam a uma temperat
Um aquecedor radiante, que é usado em processos de tratamento de superfícies, é constituído por um longo elemento aquecedor com formato cilíndrico e diâmetro D1 = 0,005 m, com emissividade ε1 = 0,80.