Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 99
Considere duas placas paralelas muito grandes. A placa inferior é mais quente do que a superior, que é mantida a uma temperatura constante de . As placas estão separadas por L = 0,1 m e no espaço entre as duas superfícies há ar à pressão atmosférica. O fluxo térmico a partir da placa inferior é de .
- Determine a temperatura da placa inferior e a razão entre os fluxos térmicos convectivo e radiante para . Calcule as propriedades do ar a T = 350 K.
- Repita a parte (a) para e .
Passo 1
Animados para seguir que eu sei, não é?
Vamos dar uma desenhada?
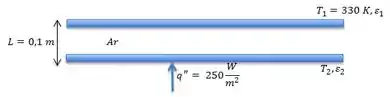
Agora que vimos o que está acontecendo podemos começar !!
A letra (a) a temperatura da placa inferior e a razão entre os fluxos térmicos convectivo e radiante para , tranquilo?
Como o fluxo de calor é composto por convecção e radiação, o fluxo total é:
O calor convectivo nós já sabemos:
Mas ainda não temos o coeficiente convectivo, não é?
Para descobrir nós podemos usar a seguinte relação:
Lembrando que:
Colocando no calor convectivo:
A taxa removida por radiação pode ser escrita como:
E substituindo no calor total:
Passo 2
Sabemos que:
Avaliando as propriedades do ar para a temperatura dada, na Tabela A – 4:
Substituindo:
Resolvendo:
Essa foi moleza, não foi? Mas ainda não terminamos ...
Passo 3
Bom, a letra (a) ainda nos pediu a razão entre os fluxos térmicos convectivo e radiante, sendo assim nós vamos substituir a temperatura e achar cada um deles:
Fazendo a razão:
Agora sim !! Finalizamos a letra (a) !!
Passo 4
Na letra (b) nós vamos repetir o que fizemos antes, mas aqui usaremos para
E achando agora os calores convectivos e radioativos:
Fazendo a razão:
Passo 5
E para finalizar a letra (b) nós vamos fazer
E achando agora os calores convectivos e radioativos:
Fazendo a razão:
Legal, não foi ?!