Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 101

Uma janela de vidro duplo tem duas placas de vidro, cada uma com espessura t = 6 mm. A temperatura no lado interior é T i   =   20 ° C , com h i =   7,7 W m 2 K , enquanto a temperatura no lado externo é T e =   – 10 ° C , com h e =   25 W m 2 K . O espaço entre as placas de vidro tem espessura L   =   5   m m e é preenchido com um gás. As superfícies do vidro podem ser

tratadas com um revestimento de baixa emissividade para reduzir sua emissividade de ε = 0,95 para ε = 0,05. Determine o fluxo térmico através da janela para: caso 1: ε 1 = ε 2   =   0,95 ; caso 2: ε 1 = ε 2   =   0,05 ; e caso 3: ε 1   =   0,05 ,     ε 2   =   0,95 . Considere que o espaço entre as placas de vidro possa ser preenchido com ar ou com argônio, que tem condutividade térmica k A r =   17,7   ×   10 – 3 W m K . Transferência de calor por radiação ocorrendo nas superfícies externas das duas placas de vidro é desprezível, assim como a convecção natural entre as duas placas.

Passo 1

Animados para seguir que eu sei, não é?

Vamos dar uma desenhada?

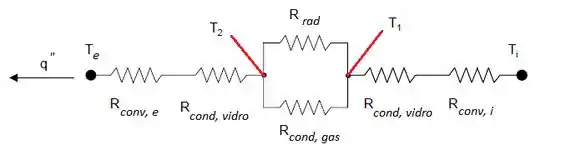
Agora que vimos o que está acontecendo podemos começar !!

Bom, nós queremos o fluxo térmico, não é? Esse fluxo vai ser a soma da troca de calor ao longo de todo o caminho:

q " = q " T i - T 1 + q " T 1 - T 2 + q " T 2 - T e

Vamos relembrar como calculamos o calor para cada situação?

q " T i - T 1 =   T i - T 1 R " c o n v , i + R " c o n d , v i d r o  

q " T 1 - T 2 = T 1 - T 2 1 R " r a d + 1 R " c o n d , g a s

q " T 2 - T e = T 2 - T e R " c o n v , e + R " c o n d , v i d r o

Nós sabemos que:

T i   =   20 ° C

  T e =   – 10 ° C

Mas nós ainda não sabemos T 1 nem T 2 , não é?

Mas vamos seguindo !!

Passo 2

Vamos relembrar como calcular as resistências?!

R " c o n v , e = 1 h e

R " c o n d , v i d r o = t k v i d r o

R " c o n d , g a s = L k g a s

R " c o n v , i = 1 h i

R " r a d = 1 ε 1 + 1 ε 2 - 1 σ T 1 2 - T 2 2 T 1 - T 2

Nós sabemos que:

t   =   6   m m

h i =   7,7 W m 2 K

h e =   25 W m 2 K

L   =   5   m m

k A r =   17,7   ×   10 – 3 W m K

Para o ar a 300 K, olhando na Tabela A – 4:

k a r =   26,3   ×   10 – 3 W m K

E para A – 3:

k v i d r o =   1,4 W m K

Substituindo:

R " c o n v , e = 1 25 W m 2 K = 0,04 m 2 K W

R " c o n d , v i d r o = 0,006   m 1,4 W m K = 0,0043   m 2 K W

R " c o n d , a r = 0,005   m 26,3   ×   10 – 3 W m K = 0,19   m 2 K W  

R " c o n d , a r g o n i o = 0,005   m 17,7   ×   10 – 3 W m K = 0 , 282   m 2 K W

R " c o n v , i = 1 7,7 W m 2 K = 0,13   m 2 K W

R " r a d = 1 ε 1 + 1 ε 2 - 1 5,67 × 10 - 8   W m 2 K T 1 2 - T 2 2 T 1 - T 2

Vamos colocar no calor?

q " T i - T 1 =   20 ° C - T 1 0,13   m 2 K W + 0,0043   m 2 K W = 20 ° C - T 1 0,13 43   m 2 K W

q " T 2 - T e = T 2 + 10 ° C 0,04 m 2 K W + 0,0043   m 2 K W = T 2 + 10 ° C 0,04 43 m 2 K W

O condutivo para o ar:

q " T 1 - T 2 ,   a r = T 1 - T 2 5,67 × 10 - 8   W m 2 K T 1 2 - T 2 2 T 1 - T 2 1 ε 1 + 1 ε 2 - 1 + 1 0,19   m 2 K W

E para o argônio:

q " T 1 - T 2 ,   a r g o n i o = T 1 - T 2 5,67 × 10 - 8   W m 2 K T 1 2 - T 2 2 T 1 - T 2 1 ε 1 + 1 ε 2 - 1 + 1 0,282   m 2 K W

Agora não tem jeito galerinha, vamos usar o software IHT para resolver estas equações simultaneamente !!

Mas não podemos nos esquecer, ε 1 e ε 2 variam para cada caso assim como o valor condutivo!!

Jogando tudo no software o que nós obtemos parar o calor total é:

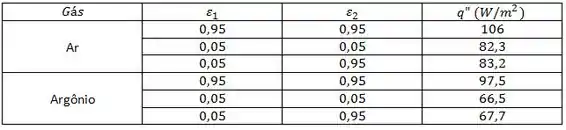
E é isso aí galerinhaaa !!

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere as condições do Problema 9.107. Levando em consideração a radiação, assim como a convecção através da cavidade preenchida com hélio, determine a taxa mássica de nitrogênio gasoso que é perdi
Um revestimento superficial especial, sobre um painel quadrado com 5 m por 5 m de lado, é curado pela colocação do painel diretamente sob uma fonte de calor radiante que tem as mesmas dimensões. A fon
Considere o Problema 9.93 com N = 4 finas folhas de alumínio (εf = 0,07), igualmente espaçadas ao longo do espaço de 50 mm, formando assim cinco espaços de ar individuais cada um com 10 mm de espessur
Um longo aquecedor na forma de bastão, com diâmetro D1 = 10 mm e emissividade ε1 = 1,0, encontra-se posicionado coaxialmente a um refletor semicilíndrico isolado termicamente com diâmetro D2 = 1 m. Um
Um gerador de vapor é constituído por um feixe alinhado de tubos, cada um com diâmetro externo D = 10 mm e comprimento L = 1 m. Os passos longitudinal e transversal são SL = ST = 20 mm, enquanto os nú