Sejam as bolas de aço do Problema 5.6, mas agora a temperatura do ar aumenta com o tempo na forma , sendo .

(a) Esboce a temperatura da bola versus o tempo para . Mostre também a temperatura ambiente, , em seu esboço. Explique características especiais do comportamento da temperatura da bola.

(b) Ache uma expressão para a temperatura da bola em função do tempo, T(t), e apresente graficamente a temperatura da bola para 0 ≤ t ≤ 1 h. O seu esboço estava correto?

(a)

Todos os dados usados são para o aço e estão presentes no final do livro.

Agora que fizemos a análise do nosso problema vamos as nossas contas, primeiro vamos calcular o número de , usando a equação . Como se trata de uma esfera .

Isso nos diz que a temperatura da esfera de metal vai se manter praticamente uniforme durante o processo de resfriamento. Agora vamos escrever a equação com o apresentado na questão.

Vamos chamar de assim , organizando nossa equação temos:

Fazendo , temos:

Resolvendo por E.D.O criamos um sistema homogêneo:

Onde .

Fazendo sendo:

Estamos quase chegando na nossa resposta não desista!

Substituindo tudo na nossa E.D.O temos:

Fazendo , , agora pra finalizar vamos substituir por , assim temos:

Só pra lembrar esse que apareceu é porque nosso é uma condição de contorno com

logo .

(b)

Vamos lá está quase acabando, nossa letra b nos pede o gráfico da equação da letra (a), usando um software vamos usar nossa equação pra analisar o decaimento da temperatura ao longo de uma hora, assim temos:

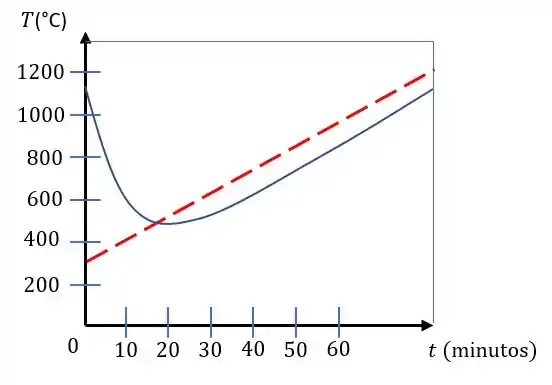
A linha azul representa a temperatura da esfera, a linha vermelha tracejada representa a temperatura ambiente

Para tempos pequenos nossa temperatura decai rapidamente pois a diferença de temperatura é grande.

Pouco antes dos 20 minutos as temperaturas da esfera e do ambiente são iguais, ou seja, não há fluxo de calor, e com o passar do tempo a diferença de temperatura é constante, isso nos diz que, o fluxo será constante.

Ufa! Finalmente terminamos!