Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 8
O coeficiente de transferência de calor para o ar escoando sobre uma esfera deve ser determinado pela observação do comportamento dinâmico da temperatura de uma esfera, que é fabricada em cobre puro. A esfera, que tem de diâmetro, encontra-se a antes de ser inserida em uma corrente de ar que tem a temperatura de . Um termopar sobre a superfície externa da esfera indica após da inserção da esfera na corrente de ar. Admita, e depois justifique, que a esfera se comporta como um objeto espacialmente isotérmico e calcule o coeficiente de transferência de calor.
Passo 1
Vamos lá! Nosso problema nos pede o valor do coeficiente de convecção, mas antes que tal desenharmos o comportamento desse problema pra entendermos o que o ocorre. Fica assim.
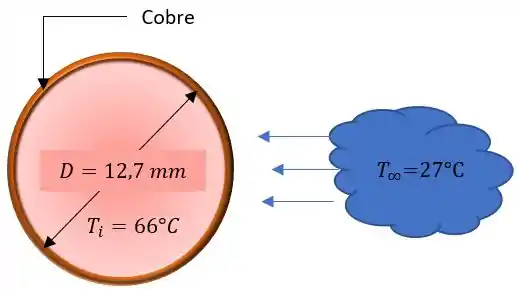
Agora vamos as nossas famosas considerações pra resolver nosso problema.
Passo 2
Vamos usar os dados da tabela pro cobre.
Agora que fizemos a análise do nosso problema vamos as nossas contas, primeiro vamos usar nossa equação .
Onde , , , , .
Substituindo temos:
Agora usando a equação .
Isolando o nosso coeficiente de convecção , temos:
Passo 3
Agora pra verificar nossa condição objeto espacialmente isotérmico vamos usar nossa equação .
Como nosso número de , a condição de objeto espacialmente isotérmico é válida!
Ufa! Finalmente terminamos!
Resposta
Como nosso número de , a condição de objeto espacialmente isotérmico é válida!