Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 74

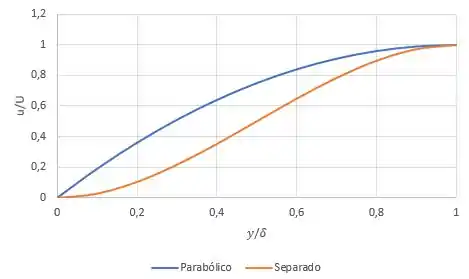
A separação da camada limite ocorre quando a tensão de cisalhamento na superfície torna-se zero. Considere uma representação polinomial para a camada limite laminar da forma u U = a + b λ + c λ 2 + d λ 3 , em que λ = y δ . Especifique condições de contorno para o perfil de velocidade na separação. Determine constantes apropriadas, a , b , c e d , para o perfil de separação. Calcule o fator de forma H na separação. Trace o perfil e compare-o com o perfil parabólico aproximado.

Passo 1

Listinha do que a gente precisa fazer:

- especificar condições de contorno para esse perfil na separação

- achar uma equação apropriada para esse perfil de velocidade polinomial

- calcular o fator de forma H na separação.

- traçar esse perfil e comparar com o perfil parabólico:

u U = 2 y δ - y δ 2

Vamos começar!

Passo 2

A gente quer que na parede o cisalhamento seja nulo.

τ w = μ d u d y = 0 ,   y = 0

Juntando isso as outras condições mais comuns da camada limite laminar, a gente pode dizer que as condições de contorno são:

- em y = 0 :

u = 0 ,     τ w = μ d u d y = 0  

- em y = δ

u = U ,     τ = μ d u d y = 0

Passo 3

Temos 4 condições para 4 constantes. Vamos achar elas:

u U = a + b λ + c λ 2 + d λ 3

- em y = 0 → λ = 0 :

u = U a + b ⋅ 0 + c ⋅ 0 + d ⋅ 0 = 0 ∴ a = 0

A gente tem definido que:

d u d y = U δ   d d y u U = U δ b + 2 c λ + 3 d λ 2

τ w = μ U δ b + 2 c ⋅ 0 + 3 d ⋅ 0 = 0 ∴ b = 0

- em y = δ → λ = 1 :

u = U c ⋅ 1 + d ⋅ 1 = U ∴ c + d = 1

τ = μ U δ 2 c ⋅ 1 + 3 d ⋅ 1 = 0 ∴ 2 c + 3 d = 0

c = 3 ,     d = - 2

Nossa expressão fica com essa carinha:

u U = 3 y δ 2 - 2 y δ 3

Passo 4

Para calcular H , a gente usa essa fórmulinha:

H = δ * θ

Aí calculando esses valores pela definição, usando nosso perfil de velocidade:

δ * = ∫ 0 δ 1 - u U d y = δ 2

θ = ∫ 0 δ u U 1 - u U d y = 9 δ 70

Logo:

H = δ 2 ⋅ 70 9 δ = 3,89

Passo 5

Por fim, traçando os dois perfis juntinhos:

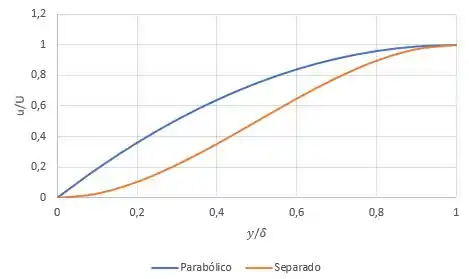
Resposta

y = 0 ,     u = 0 ,     τ w = μ d u d y = 0  

y = 0 ,     u = U ,     τ = μ d u d y = 0

u U = 3 y δ 2 - 2 y δ 3

H = 3,89

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma esfera de cerâmica lisa (densidade = 2,6) é imersa em um escoamento de água a 20°C e 25 cm/s. Qual será o diâmetro da esfera se ela se deparar (a) com escoamento muito lento (creeping flow), Red =
Repita a análise de quantidade de movimento sobre aplaca plana da Seção 7.2 substituindo o perfil parabólico, Equação (7.6), por um perfil senoidal mais exato:u/U =sen(piy/2delta)Calcule estimativas d
A forma de perfil de velocidade u/U = 1 – exp(–4,605y/d) é uma curva suave com u = 0 em y = 0 e u = 0,99U em y 5 d e, sendo assim, parece ser um substituto razoável do perfil parabólico para placa pla
Ar, rho= 1,2 kg/m3 e mu =1,8 E-5 kg/(m s) escoa a 10 m/s sobre uma placa plana. No bordo de fuga da placa, foram medidos os seguintes dados do perfil de velocidades:Se a superfície superior tem uma ár
Deduza formas modificadas das equações de camada-limite laminar (7.19) para o caso de escoamento axialmente simétrico ao longo da superfície externa do cilindro circular de raio constante R, como na F