Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 24

Dois fluidos imiscíveis estão contidos entre placas paralelas infinitas. As placas estão separadas pela distância 2h, e as duas camadas de fluidos têm a mesma espessura h = 5   m m . A viscosidade dinâmica do fluido superior é quatro vezes aquela do fluido inferior, que é μ i n f e r i o r = 0,1   N · s / m 2 . Se as placas são estacionárias e o gradiente de pressão aplicado for - 50   k P a / m , encontre a velocidade na interface. Qual é a velocidade máxima no escoamento? Trace um gráfico da distribuição de velocidade.

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Este problema nos pede para determinarmos a velocidade na interface e, depois, a velocidade máxima no escoamento. Por fim, traçar um gráfico da distribuição da velocidade. Primeiro, temos:

τ + d d y τ ∙ d y 2 - τ - d d y τ ∙ d y 2 d x d z + p - d d x p ∙ d x 2 - p - d d x p ∙ d x 2 d y d z = 0

Simplificando:

d τ d y = d p d x = k  

Logo, para cada fluido, temos:

μ d 2 d y 2 u = k

Aplicando aos fluidos 1 e 2, ficamos com:

u 1 = k 2 μ 1 y 2 + c 1 y + c 2

u 2 = k 2 μ 2 y 2 + c 3 y + c 4

Para as condições de contorno, temos:

y = - h u 1 = 0

E também, para o fluido 1, temos:

y = 0 u 1 = u 2

Para o fluido 2:

  y = h

u 2 = 0

Logo:

μ 1 d u 1 d y = μ 2 d u 2 d y

Com isso, temos:

0 = k 2 μ 1 h 2 - c 1 h + c 2

Onde c 2 = c 4 . Portanto:

0 = k 2 μ 2 h 2 + c 3 h + c 4 μ 1 c 1 = μ 2 c 3

Consequentemente, temos que:

c 1 = k h 2 μ 1 ( μ 2 - μ 1 ) ( μ 2 + μ 1 )   c 2 = - k h 2 μ 2 + μ 1

c 3 = k h 2 μ 2 μ 2 - μ 1 μ 2 + μ 1 c 4 = c 2  

Substituindo:

c 1 = - 750 1 s   c 2 = 2,5   m / s

c 3 = - 187,5   1 s c 4 = 2,5   m / s

Passo 2

Agora, para as distribuições de velocidade, temos:

u 1 y = k 2 μ 1 y 2 + y h μ 2 - μ 1 μ 2 + μ 1 - k h 2 μ 2 + μ 1

Para o fluido 2:

u 2 y = k 2 μ 2 y 2 + y h μ 2 - μ 1 μ 2 + μ 1 - k h 2 μ 2 + μ 1

Passo 3

Por fim, para a velocidade em y = 0 , temos:

u = - k h 2 μ 2 + μ 1 u = 2,5   m / s

E o nosso gráfico de distribuição de velocidade vai ficar assim:

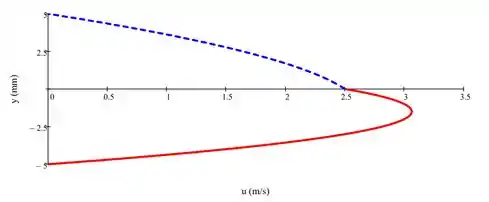
Resposta

u 1 y = k 2 μ 1 y 2 + y h μ 2 - μ 1 μ 2 + μ 1 - k h 2 μ 2 + μ 1

u 2 y = k 2 μ 2 y 2 + y h μ 2 - μ 1 μ 2 + μ 1 - k h 2 μ 2 + μ 1

u = 2,5   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Querosene é bombeado através de um tubo liso com diâmetro interno D = 30 mm, na proximidade do número de Reynolds crítico. O escoamento é instável e flutua entre os estados laminar e turbulento, fazen
Foi sugerido, no projeto de um “sprinkler” agrícola, que um elemento estrutural fosse mantido fixo por meio de um arame esticado ao longo da linha de centro de um tubo; acreditava-se que um arame rela
A seguinte solução: u = u 0 1 - y 2 a 2 - z 2 b 2 pode ser usada como um modelo para o perfil de velocidade de um escoamento pressurizado completamente desenvolvido em um canal com seção transversal e
Um medicamento líquido, com a viscosidade e a massa específica da água, deve ser administrado através de uma agulha hipodérmica. O diâmetro interno da agulha é 0,25 mm e o seu comprimento é de 50 mm.
O clássico escoamento de Poiseuille (Eq. 8.12) mostra a condição de não deslizamento na parede. Se o fluido é um gás, e quando o livre caminho médio l (distância média que uma molécula viaja antes de