Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 2.Exercício - Ex. 12
No sistema da figura, se a escala fornece em , qual é o valor real, em , de uma divisão da escala? Dados: ; ; .
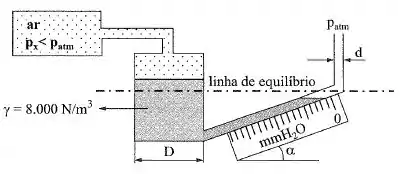
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão. O enunciado pede o valor em , de uma divisão da escala, certo? E o que isso quer dizer… Bom, ele quer o comprimento , desse sistema, ok? Vamos lá então!
Vamos começar lembrando que o somatório das pressões é dado por:
Opa! Então vamos ter:
Beleza! Mas e esse ? Bom, lembra que o enunciado falou que depende da escala… Então vamos olhar para aquela régua que está em … Dá só uma olhada, o nível está marcando um tracinho antes o zero, né?
Opa! Então tá tudo ok! Vamos ter que:
Substituindo então na equação, ficaremos com:
Passo 2
Na posição em que se encontram os comprimentos, teremos a seguinte relação:
Logo:
Passo 3
Agora a gente pode substituir esse na equação e ficar com:
Vamos então isolar o , porque é ele que nós queremos encontrar, e teremos:
Substituindo nossos valores, temos que:
Show! Podemos cortar esse e ficaremos com:
Opa! Então temos:
Prontinho!