Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 2.Exercício - Ex. 1

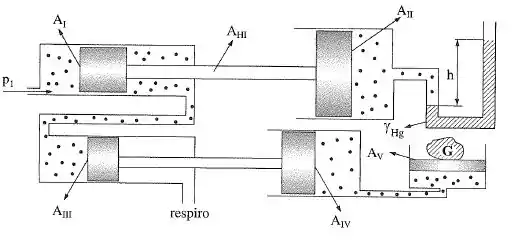
No sistema da figura, desprezando-se o desnível entre os cilindros, determinar o peso G , que pode ser suportado pelo pistão V . Desprezar os atritos. Dados: p 1 = 500   k P a ; A I = 10   c m 2 ; A H I = 2   c m 2 ; A I I = 2,5   c m 2 ; A I I I = 5   c m 2 ; A I V = 20   c m 2 ; A V = 10   c m 2 ; h = 2   m ; γ H g = 136.000   N / m 3 .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Para encontrar o peso suportado pelo pistão precisamos encontrar a pressão nos pontos 3 e 4 . Temos que:

p 1 A I = p 3 A I - A H I + p 2 A I I

Logo:

p 3 = p 1 A I - P 2 A I I A I - A H I

Note que todas as variáveis foram dadas no problema, EXCETOOOOO a P2!! E como a gente calcula esse treco? Bem, a gente sabe que a pressão de coluna de mercúrio é a responsável pela pressão que é exercida na A I I , certo?

Mas como a gente calcula mesmo a pressão hidrostática? Opaaaaaaa!!!!!

P h i d r o s t á t i c a = ρ g h

Mas o problema ainda foi legal com a gente, ele já deu o valor de ρ H g g = γ H g = 136000   N / m ²

Então ao final nossa equação fica da seguinte forma:

p 3 = p 1 A I - γ H g h A I I A I - A H I

Substituindo os valores, temos que:

p 3 = 500000 10 - ( 136000 × 2 ) ( 2,5 ) 10 - 2

p 3 = 540000   P a

Também temos a relação:

p 4 A I V = p 3 A I I I

p 4 = 540000 5 20

p 4 = 135000   P a

Passo 2

Com a pressão p 4 , podemos então determinar o peso de G :

G = p 4 A V

G = 135000 10 ⋅ 10 - 4

G = 135   N

Resposta

G = 135   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Qual é a diferença entre pressão manométrica e pressão absoluta?
Alguém diz que a pressão absoluta de um líquido de densidade constante dobra quando a profundidade dobra. Você concorda? Explique.
Um pequeno cubo de aço está suspenso na água por uma corda. Se os comprimentos das laterais do cubo forem muito pequenos, como você compararia as imensidades das pressões na parte superior, inferior e
Considere dois ventiladores idênticos, um no nível do mar e o outro no alto de uma montanha, trabalhando a velocidades idênticas. Como você compararia :as vazões volumétricasas vazões mássicas dos ven
A água de um tanque é pressurizada a ar, e a pressão é medida por um manômetro de vários fluidos, como mostra a figura. Determine a pressão manométrica do ar no tanque se h 1 = 0,2m , h 2 = 0,3m e h 3