Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 45

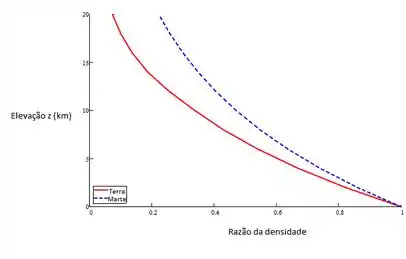
Uma atmosfera de Marte se comporta como um gás ideal com massa molecular média de 32,0 e temperatura constante de 200 K. A massa específica da atmosfera na superfície do planeta = 0,015kg/m³ e gravidade igual a 3,92m/s². Calcule uma massa específica da atmosfera Marciana em uma altitude z = 20 km acima da superfície. Rastrear um gráfico da razão entre uma massa específica e uma massa específica na superfície como uma função da elevação. Compare o resultado com os dados da atmosfera terrestre.

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Primeiramente, sabemos que:

d p d z = - ρ g

p = ρ R T

R = R u M m

Derivando a equação de estado:

d p = R   T   d ρ

Combinando com as equações acima, teremos:

R T d ρ d z = - ρ g

Portanto:

d ρ ρ = - g R T d z

Agora, precisamos integrar a expressão e aplicar os limites de integração:

∫ ρ 0 ρ 1 ρ d ρ = - ∫ 0 z g R T d z

Logo:

ln ⁡ ρ ρ 0 = - g z R T

ρ ρ 0 = e - g z R T

Agora, podemos substituir os valores para obtermos a densidade:

ρ = 3,32 × 10 - 3   k g / m 3

Passo 2

Agora, precisamos plotar o gráfico pedido. Para facilitar, vamos fazer a seguinte substituição:

x = g R T → x = 0,07544   k m - 1

Logo:

ρ ρ 0 = e - x z

Agora, basta plotar o gráfico substituindo os dados da tabela A.3:

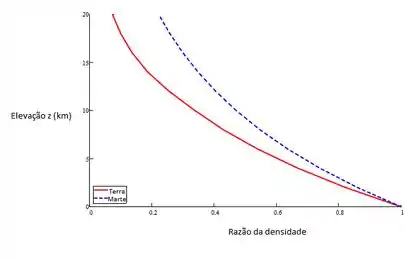
Resposta

ρ = 3,32 × 10 - 3   k g / m 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A carga de 500 kg do macaco hidráulico mostrado na figura abaixo deve ser elevada despejando-se óleo ( ρ = 780k g / m ³ ³) dentro de um tubo fino. Determine quão alto h deve ser para começar a levanta
Considere um tubo em U cujos braços estão abertos para a atmosfera. Água é despejada no tubo em U de um braço, e óleo leve ( ρ = 790k g / m ³ ³) do outro. Um braço contém 70 cm de altura de água, enqu
Água doce e água do mar escoam em tubulações horizontais paralelas que estão conectadas entre si por um manômetro de tubo em U, como mostrado abaixo. Determine a diferença de pressão entre as duas tub
Na figura P2.12 o tanque contém água e óleo imiscíveis a 20 °C. Qual é o valor de h em cm se a massa específica do óleo é de 898 k g / m 3 ?
Na figura P2.13 as superfícies da água e da gasolina a 20°C estão abertas à atmosfera e na mesma elevação. Qual é a altura h do terceiro líquido no ramo direito?