Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Sistemas de Controle - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 68

Uma sólida represa de concreto deve ser construída de modo a reter água até uma profundidade D . Para facilitar a construção, as paredes da represa devem ser planas. Sua supervisora solicita que você considere as seguintes seções transversais para a represa: um retângulo, um triângulo retângulo com a hipotenusa em contato com a água e um triângulo retângulo com um cateto vertical em contato com a água. Ela quer que você determine quais dessas três seções requer a menor quantidade de concreto. O que estará escrito em seu relatório? Você decide estudar uma possibilidade a mais: um triângulo qualquer conforme mostrado. Desenvolva e trace um gráfico de uma expressão para a área da seção transversal A como função de α , e determine a área mínima requerida da seção transversal.

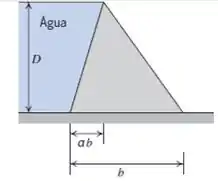
Passo 1

Diagrama de forças da represa com uma seção retangular de concreto:

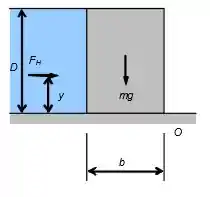
Considerando as forças horizontais agindo na represa:

F H = p ⋅ A c

F H = ρ g D 2 ⋅ w D = D 2 2 ⋅ ρ g w

Onde:

p = P r e s s ã o   a g i n d o   n a   r e p r e s a ;

A c = Á r e a   d a   r e p r e s a .

Agora, calcularemos a distância do ponto de aplicação da força hidrostática:

y = D - y '

y = D - y c + I x x A c ⋅ y c

y = D - D 2 + w D 2 12 w ⋅ D ⋅ D 2 = D - 2 D 3

y = D 3

Onde:

y ' = D i s t â n c i a   d o   c e n t r o   a t é   a   s u p e r f í c i e   l i v r e ;

y c = d i s t â n c i a   d o   c e n t r o   d a   r e p r e s a ;

I x x = M o m e n t o   d e   i n é r c i a .

O peso do concreto da represa se dá:

W = m g = S G ⋅ ρ ⋅ b w D ⋅ g

Passo 2

Analisando o momento agindo sobre o ponto O .

Sabendo que o momento devido à força hidrostática é igual ao momento ocasiona pelo próprio peso da represa, temos:

∑ M O = 0

F H ⋅ y = W ⋅ b 2

Substituindo os termos:

D 2 2 ⋅ ρ g w ⋅ D 3 = S G ⋅ ρ ⋅ b w D ⋅ g ⋅ b 2

Isolando a largura, b :

b = D 3 ⋅ S G

Obtendo S G do concreto pela Tabela A.1:

b = D 3 ⋅ 2,4 = 0,3726 ⋅ D

Obtendo a área mínima da represa na seção de corte:

A = b ⋅ D = 0,3726 ⋅ D ⋅ D = 0,3726 ⋅ D 2

Passo 3

Diagrama de forças de uma represa com seção triangular de concreto:

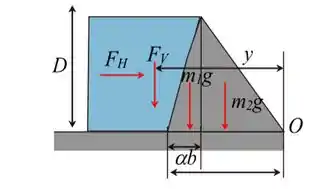
Considerando as forças horizontais agindo na represa:

F H = p ⋅ A c

F H = ρ g D 2 ⋅ w D = D 2 2 ⋅ ρ g w

A distância do ponto de aplicação da força hidrostática horizontal:

y = D - y '

y = D - y c + I x x A c ⋅ y c

y = D - D 2 + w D 2 12 w ⋅ D ⋅ D 2 = D - 2 D 3

y = D 3

Considerando as forças verticais agindo na represa:

F V = p ⋅ V ⋅ g

F v = ρ ⋅ 1 2 ⋅ α b ⋅ w ⋅ D ⋅ g

A distância do ponto de aplicação da força hidrostática vertical:

x = b - α b + 2 3 α b = b 1 - α 3

Sendo α a inclinação da seção triangular.

O peso do concreto se dá:

W = W 1 + W 2

W = m 1 g + m 2 g

W = S G ⋅ ρ ⋅ α b ⋅ w ⋅ D ⋅ g + S G ⋅ ρ ⋅ 1 - α b ⋅ w ⋅ D ⋅ g

Passo 4

Analisando o momento agindo sobre o ponto O .

Sabendo que o momento devido à força hidrostática é igual ao momento ocasiona pelo próprio peso da represa, temos:

∑ M O = 0

F H ⋅ y - F V ⋅ x = W 1 ⋅ b 1 - 2 α 3 + W 2 ⋅ 2 3 b 1 - α

D 2 2 ⋅ ρ g w ⋅ D 3 - α b ⋅ D 2 ⋅ ρ w g ⋅ b 1 - α 3 = S G ⋅ α b ⋅ ρ D w g ⋅ b 1 - 2 α 3 + [ S G ⋅ ρ w D g ⋅ 1 - α b ] ⋅ 2 3 b 1 - α

Isolando b :

b = D 3 α - α 2 + S G ⋅ 2 - α

Passo 5

Considerando, um triângulo retângulo com a hipotenusa em contato com a água ( α = 1 ) .

Sendo S G c o n c r e t o = 2,4 :

b = D 3 ⋅ 1 - 1 2 + 2,4 ⋅ 2 - 1 = 0,456 ⋅ D

Obtendo a área mínima da seção de corte:

A = b 2 ⋅ D = 0,4 5 6 ⋅ D 2 ⋅ D = 0 , 228 ⋅ D 2

Passo 6

Considerando, um triângulo retângulo com um cateto vertical em contato com a água ( α = 0 ) .

Sendo S G c o n c r e t o = 2,4 :

b = D 3 ⋅ 0 - 0 + 2,4 ⋅ 2 - 0 = 0,476 ⋅ D

Obtendo a área mínima da seção de corte:

A = b 2 ⋅ D = 0,476 ⋅ D 2 ⋅ D = 0,238 ⋅ D 2

Passo 7

A área mínima para a seção de corte de um triângulo qualquer:

A = b 2 ⋅ D = 1 2 ⋅ D 3 α - α 2 + S G ⋅ 2 - α ⋅ D

A = D 2 2 3 α - α 2 + S G ⋅ 2 - α

Assim, a razão da área pelo quadrado do diâmetro se dá:

A D 2 = 1 2 3 α - α 2 + S G ⋅ 2 - α

Passo 8

Traçando um gráfico de uma expressão para a área da seção transversal A como função de α :

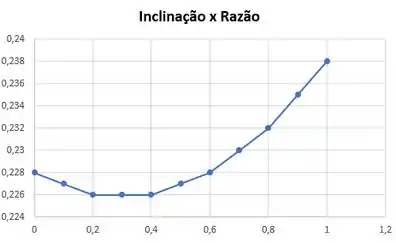
Passo 9

Determinando a área mínima requerida da seção transversal:

A = D 2 2 3 α - α 2 + S G ⋅ 2 - α

Temos que a menor razão A / D 2 obtida se dá em α = 0,3 , então:

A = D 2 2 3 ⋅ 0,3 - 0,3 2 + 2,4 ⋅ 2 - 0,3

A = 0,226 ⋅ D 2

Resposta

A r e t â n g u l o = 0,3726 ⋅ D 2

A h i p o t e n u s a = 0,228 ⋅ D 2

A c a t e t o = 0,238 ⋅ D 2

A t r i â n g u l o = 0,226 ⋅ D 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma comporta retangular (de largura w = 2 m) é articulada conforme mostrado, com um batente na borda inferior. Em que profundidade H a comporta estará prestes a abrir?
A comporta mostrada tem 1,5 m de largura e é articulada em O; a=1,0m – 2 , D=1,20m e H=1,40m . Determine (a) o módulo e o momento da componente vertical da força em torno de O, e (b) a força horizonta
Uma represa deve ser construída usando a seção transversal mostrada. Suponha que a largura da represa seja w = 50 m. Para uma altura de água H = 2,5 m calcule o módulo e a linha de ação da força verti
A comporta parabólica mostrada na figura tem 2 metros de largura e é articulada em O ; c = 0,25m - 1 , D = 2m e H = 3m . Determine (a) o módulo e a linha de ação da força vertical sobre a comporta cau