Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 6

O tubo mostrado está cheio com mercúrio a 20°C. Calcule a força aplicada no pistão

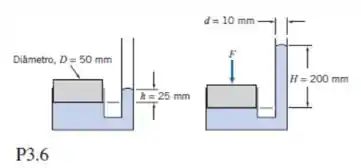
Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Este problema nos pede a aplicada no pistão. Para resolvermos, temos que a variação da pressão hidrostática é dada por:

p = p a t m - ρ g y - y 0

Sendo p y 0 = p a t m . Com isso, no estado inicial, temos:

p 1 = p a t m + ρ g h

F 1 = p 1 ∙ A F 1 = ρ g h A

Portanto:

∑ F y = 0 F 1 - W = 0 W = F 1 = ρ g h A

E para p 2 :

p 2 = p a t m + ρ g H F 2 = p 2 A = ρ g H A

Logo:

∑ F y = 0 F 2 - W - F = 0 F = F 2 - W = ρ g H A - ρ g h A = ρ g A H - h F = ρ H 2 O ∙ S G ∙ g π d 2 4 H - h

Sendo S G = 13,54 , temos:

F = 1000 k g m 3 × 13,54 × 9,81 × m s 2 × π 4 0,05   m 2 × 0,2 - 0,025 m × N s 2 k g ∙ m F = 45,6   N

Resposta

F = 45,6   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na figura abaixo o tanque e o tubo estão abertos a atmosfera. Se L = 2,13 m, qual é o ângulo de inclinação ϕ do tubo?
Um artigo interessante foi publicado no AIAA Journal em 1992. Os autores explicam que o ar no interior de um tubo plástico novo pode ser até 25% mais denso do que aquele das vizinhanças, devido ao esc
Na figura abaixo o ramo direito do manômetro está aberto à atmosfera. Determine a pressão manométrica em Pa, no espaço com ar no tanque.
Na figura abaixo as pressões em A e B são as mesmas, 100 kPa. Se for colocada mais água em A para aumentar pA para 130 kPa, determine as novas posições dos meniscos de mercúrio. O tubo de conexão tem
Diferenças de pressão muito pequenas pA – pB podem ser medidas com precisão pelo manômetro diferencial de dois fluidos como mostra abaixo. A massa específica ρ 2 é apenas ligeiramente maior do que a m