Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 12.Problemas - Ex. 27

A emissividade direcional espectral de um material difuso a 2 5 00   K apresenta a seguinte distribuição:

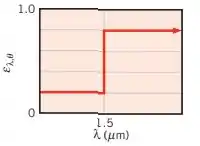
Determine a emissividade hemisférica total a 2 5 00   K . Determine o poder emissivo na faixa espectral compreendida entre 0,8 e 2,5   μ m e nas direções 0 ≤ θ ≤ 15 ° .

Passo 1

E aí, tudo bem?

Bora resolver essa questão juntos?

Se ajeite aí e vamos lá!

Começamos o nosso problema analisando que como a superfície é difusa, ε λ , θ , é independente da direção; da Eq. 12.42, ε λ , θ = ε λ .

Utilizando a Eq. 12.43, temos:

ε T = ∫ 0 ∞ ε λ λ E λ , b λ , T d λ E b T

Abrindo:

E T = ∫ 0 1,5 ε 1 E λ , b λ , 2500 d λ E b + ∫ 1,5 ∞ ε 2 E λ , b λ , 2500 d λ E b

Escrevendo agora em termos de F 0 → λ , pela Tabela 12.2:

F 0 → 1,5 = 0,2732

λ T = 1,5 ⋅ 2500 = 3750   μ m ⋅ K

Assim, temos que a emissividade hemisférica total a 2500   K :

ε 2500   K = ε 1 F 0 → 1,5 + ε 2 1 - F 0 → 1,5

ε 2500   K = 0,2 ⋅ 0,2732 + 0,8 ⋅ 1 - 0,2732

ε 2500   K = 0,636

Passo 2

Para os limites espectrais e geométricos prescritos a partir de uma equação semelhante à Eq. 12.15:

∆ E = ∫ 0,8 2,5 ∫ 0 2 π ∫ 0 π 6 ε λ , θ I λ , b λ , T cos ⁡ θ sin ⁡ θ d θ d ϕ d λ

Onde I λ , e λ , θ , ϕ = ε λ , θ I λ , b λ , T .

Sendo a superfície difusa, ε λ , θ = ε λ , e observando I λ , b é independente da direção e igual a E λ , b π , podemos escrever:

∆ E = ∫ 0 2 π ∫ 0 π 6 cos ⁡ θ sin ⁡ θ d θ d ϕ E b T π ∫ 0,8 1,5 ε 1 E λ , b λ , T d λ E b T + ∫ 1,5 2,5 ε 2 E λ , b λ , T d λ E b T  

Em termos de F 0 → λ , temos:

∆ E = ϕ 0 2 π ⋅ sin 2 ⁡ θ 2 0 π 6 σ T 4 π ε 1   F 0 → 1,5 - F 0 → 0,8 + ε 1   F 0 → 2 , 5 - F 0 → 1,5

Passo 3

Pela Tabela 12.2:

λ T = 0,8 ⋅ 2500 = 2000   μ m ⋅ K e F 0 → 0,8 = 0,067

λ T = 2,5 ⋅ 2500 = 6250   μ m ⋅ K e F 0 → 2,5 = 0,7 60

Substituindo os dados:

∆ E = 2 π ⋅ sin 2 ⁡ π 6 2 ⋅ 5,67 × 10 - 8 ⋅ 2500 4 π ⋅ [ 0,2 ⋅ 0,2732 - 0,067 + 0,8 ⋅ 0,760 - 0,2732 ]

∆ E = 79,66   W / m 2

Te espero na próxima questão!

Resposta

ε 2500   K = 0,636

∆ E = 79,66   W / m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A função de emissividade espectral de uma superfície opaca a 1000 K é aproximada como: ε λ = ε 1 = 0,4 , 0 ≤ λ3μ m ε 2 = 0,7 ,3μ m ≤ λ6μ m ε 3 = 0 , 3 ,6μ m ≤ λ∞ Determine a emissividade média da supe
Uma pequena superfície de área A 1 = 5 cm2 emite radiação como um corpo negro a T 1 = 1000 K. Um sensor de radiação de área A 2 = 3 cm2 é colocado na direção normal da visualização da superfície A 1 n
A emissividade de um filamento de tungstênio pode ser aproximada como 0,5 para radiação em comprimentos de onda menores que 1 μ m e 0,15 para radiação superior a 1 μ m. Determine a emissividade média
A refletividade do alumínio revestido com sulfato de chumbo é 0,35 para uma radiação com comprimentos de onda inferiores a 3 μ m e 0,95 para uma radiação superior a 3 μ m. Determine a refletividade mé
As variações da emissividade espectral de duas superfícies são indicadas na figura a seguir. Determine a emissividade média de cada superfície a T =3.000 K. Além disso, determine a absortividade e a r