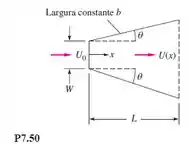
Considere o difusor de paredes planas na Figura P7.50, que é semelhante àquele da Figura 6.26a com largura constante b. Se x é medido a partir da entrada e as camadas-limites nas paredes são finas, mostre que a velocidade no núcleo do difusor é dada aproximadamente por

em que é a altura na entrada. Use essa distribuição de velocidades com o método de Thwaites para calcular o ângulo em que a separação laminar ocorrerá no plano de saída quando o comprimento do difusor for . Observe que o resultado é independente do número de Reynolds.

Bora fazer mais umazinha!

Cara, nós podemos aproximar em uma dimensão pela relação de continuidade, assim:

ou,

Caímos na solução de Görtler do prob 7.48, retornando nela com , teremos:

Se,

ou,

Por separação!

Assim,