Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 105
Na tabela 7.2, o coeficiente de arrasto de um cilindro elíptico 4:1, para escoamento laminar na camada limite é 0,35. Segundo Patton [17], a massa hidrodinâmica desse cilindro é , em que b é a largura para dentro do papel e h é a espessura máxima. Use esses resultados para deduzir uma fórmula para a evolução temporal U(t) do cilindro se ele for acelerado desde o repouso, através de um fluido parado, pela aplicação súbita de uma força constante F.
Passo 1
E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)! Primeiro passo é DESENHAR!!!
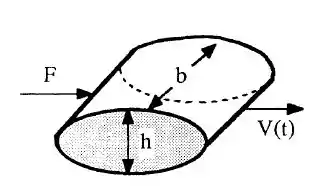
Passo 2
A equação do movimento diz que:
Passo 3
Separando e integrando, temos que:
Onde
Resposta
Exercícios de Livros Relacionados
Considere um escoamento bidimensional: u = a x + b y e v = c x + d y , em que a ,b ,c e d são constantes. Se o escoamento for incompressível e irrotacional, encontre a relação entre a , b , c e d . En
O campo de velocidade para um escoamento bidimensional é V → = A x - B y t i → - ( B x + A y ) j → , em que A = 1s - 2 ,B = 2s - 2 ,t é dado em segundos e as coordenadas são medidas em metros. Este é
Num plano, o escoamento de um fluido é definido por: v x = v 0 x + a t ; v y = v 0 y. Determinar:As linhas de correnteAs trajetórias
Sendo v x = 4 x - 6 y ; v y = k y - f ( x ) , determinar k e f(x) para que este seja um campo de velocidades de um escoamento irrotacional de um fluido incompressível. Determinar as funções de corrent
Dado o campo de velocidades v → = 13 x 2 + y e x → + 10 e y → + y z 2 e z → Qual é a velocidade angular do elemento fluido na posição definida pelo vetor r → = 6 e x → + 3 e → y + 2 e → z ?É possível