Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 1.Problemas - Ex. 2
A Tabela A.6 lista a massa específica da atmosfera padrão como uma função da altitude. Utilize esses valores para estimar grosseiramente — digamos, dentro de um fator de 2 — o número de moléculas de ar em toda a atmosfera da terra.
Passo 1
O enunciado pede para usarmos a Tabela A.6 do livro, nela tem os valores de altitude e a massa específica para cada um desses valores, exatamente como uma função.
Como a atmosfera é dividida em camadas (troposfera, mesosfera, etc.), vamos pegar a primeira, que vai de a de altitude. Então usamos os pontos da tabela para descrever a função de massa específica, ela se parece com uma exponencial:
Onde é uma constante de ajuste que tem unidade e valor próximo de , e é a altitude.
Passo 2
Agora fazemos a integral da massa específica desde a superfície da Terra até os de altitude, mas para isso precisamos considerar o raio da Terra na equação, que chamaremos de :
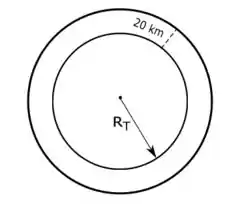
Assim:
O representa a área da superfície da Terra, e é o ponto de altitude zero
Integramos de zero a infinito por causa da forma da exponencial que deduzimos anteriormente, como a exponencial é negativa, ela vai a zero no infinito, então a soma sobre todos os vai dar para a gente a massa total de todas as moléculas de ar que compõem a atmosfera
Se considerarmos que o raio da terra é aproximadamente:
E que é o primeiro valor da tabela, além do que vem da equação deduzida de , a equação fica:
Que resulta em:
Passo 3
Agora precisamos da massa de ar por mol, que é:
Se dividirmos pelo número de Avogadro, teremos o número total de moléculas para um mol de ar:
Depois só dividir a massa total de ar que calculamos no Passo 2 por esse valor, com isso, teremos o número de moléculas estimado: