Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 77

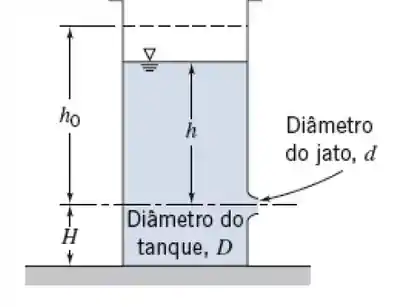
O tanque, de diâmetro D, tem um orifício arredondado e liso de diâmetro d . Em t = 0 , o nível da água está na altura h 0 . Desenvolva uma expressão para a relação adimensional entre a altura instantânea e a altura inicial da água, h / h 0 . Para D / d = 10 , trace um gráfico de h / h 0 como uma função do tempo com h 0 como parâmetro para 0,1 ≤ h 0 ≤ 1   m . Para h 0 = 1   m , trace um gráfico de h / h 0 como uma função do tempo com D / d como parâmetro para 2 ≤ D / d ≤ 10 .

Passo 1

Tá legal! Vamos começar o exercício aplicando o princípio da continuidade para o sistema, pois nós sabemos que toda a água que sai pelo orífico, corresponde ao nível de água que abaixou do tanque, então, temos:

Q t = Q j

v t A t = v j A j → v t π D 2 4 = v j π d 2 4 → v j = v t D d 2

Agora vamos aplicar Bernoulli entre a superfície do tanque (ponto 1) e o ponto de saída do orifício (2), então, temos:

p 1 ρ + v t 2 2 + g z 1 = p 2 ρ + v j 2 2 + g z 2

Nesse caso, como a superfície do tanque e a saída do jato (ponto 1) estão expostos ao ambiente, então p 1 = p 2 = p a t m e os termos de pressão se cancelam. Sabemos que as alturas são z 1 = H + h e z 2 = H , então, a equação se torna:

v t 2 2 + g H + h = v t D d 2 2 2 + g H

Agora vamos manipular a equação para isolar v t :

v t 2 2 - v t 2 2 D d 4 = g H - g H - g h → v t 2 2 1 - D d 4 = - g h

v t 2 2 D d 4 - 1 = g h → v t = 2 g h D d 4 - 1

Passo 2

Sabemos que a velocidade da descida da água no tanque corresponde a variação de altura pela variação no tempo, e na forma diferencial, podemos escrever:

v t = - d h d t

Então, igualando essa expressão à última equação do passo 1, temos:

2 g h D d 4 - 1 = - d h d t → d h h = - 2 g D d 4 - 1 d t

Integrando essa expressão dos dois lados, temos:

∫ 0 h d h h = ∫ 0 t - 2 g D d 4 - 1 d t

2 h 1 2 = - 2 g D d 4 - 1 t + C

Para descobrir o valor da constante C, sabemos que para o tempo t = 0 , temos a altura do tanque h 0 , então, substituindo esses valores na expressão anterior:

2 h 0 1 2 = - 2 g D d 4 - 1 0 + C → C = 2 h 0 1 2

Dessa forma, a equação se torna:

2 h 1 2 = - 2 g D d 4 - 1 t + 2 h 0 1 2

E, isolando h / h 0 na expressão acima para depois analisarmos os gráficos conforme dito no enunciado, vamos dividir toda a equação por 2 h 0 1 / 2 , então, temos:

2 h 1 2 2 h 0 1 2 = - 2 g D d 4 - 1 t 2 h 0 1 2 + 1 → h 1 2 h 0 1 2 = - 2 g 4 h 0 D d 4 - 1 t + 1

Elevando os dois lados ao quadrado, temos:

h h 0 = 1 - g 2 h 0 D d 4 - 1 t 2

Passo 3

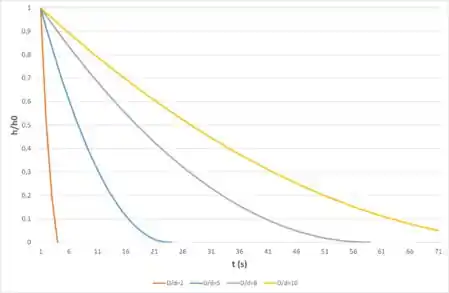
Agora vamos plotar o gráfico de h / h 0 para D / d = 10 , como uma função do tempo com h 0 como parâmetro para 0,1 ≤ h 0 ≤ 1   m :

Passo 4

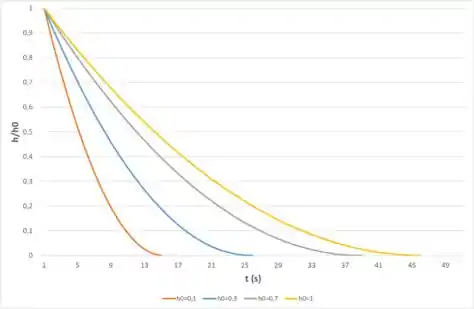
Agora vamos plotar o gráfico de h / h 0 para h 0 = 1   m como uma função do tempo com D / d como parâmetro para 2 ≤ D / d ≤ 10 .

Resposta

h h 0 = 1 - g 2 h 0 D d 4 - 1 t 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Problem C6.9 gives data for a proposed Alaska-to-Canadanatural gas (assume CH4) pipeline. If the design fl ow rate is890 kg/s and the entrance conditions are 2500 lbf/in2 and1408F, determine the maxim
Natural gas, approximated as CH4, fl ows through a Schedule 40 six-inch pipe from Providence to Narragansett, RI, adistance of 31 miles. Gas companies use the barg as a pressure unit, meaning a bar of
Air flows through a rough pipe 120 ft long and 3 in indiameter. Entrance conditions are p 5 90 lbf/in2, T 5 688F,and V 5 225 ft/s. The fl ow chokes at the end of the pipe.(a) What is the average frict
Air flows adiabatically, with f 5 0.024, down a long6-cm-diameter pipe. At section 1, conditions are T1 5300 K, p1 5 400 kPa, and V1 5 104 m/s. At section 2,V2 5 233 m/s. (a) How far downstream is sec
Steam, in a tank at 300 kPa and 600 K, discharges isentropically to a low-pressure atmosphere through a convergingnozzle with exit area 5 cm2. (a) Using an ideal gasapproximation from Table B.4, estim