Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 82
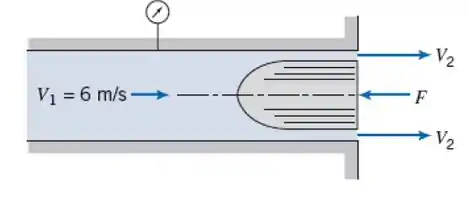
Água escoa, com baixa velocidade, através de um tubo circular com diâmetro interno de 50 mm. Um tampão arredondado e liso, de 38 mm de diâmetro, é mantido na extremidade do tubo onde a água é descarregada para a atmosfera. Ignore efeitos de atrito e considere perfis uniformes de velocidade em cada seção. Determine a pressão medida pelo manômetro e a força requerida para manter o tampão no lugar.
Passo 1
Tá legal! Vamos começar o exercício aplicando a equação de Bernoulli entre o ponto no escoamento (1) e a saída de fluido (2):
Como o enunciado não mencionou, podemos desprezar a diferença entre as cotas e . E como a saída está exposta a atmosfera, então temos e dessa forma iremos obter uma pressão manométrica. Então, reescrevendo a equação, temos:
Agora, podemos aplicar o princípio da continuidade para o sistema e igualar as vazões na tubulação e na saída, então:
Então, substituindo os valores conhecidos, temos:
Passo 2
Agora podemos retornar à equação da pressão do passo 1 e substituir os valores conhecidos:
Passo 3
Agora para encontrar a força requerida para manter o tampão no lugar, vamos aplicar o equilíbrio de momento, da equação 4.18a para o sistema, a equação tem a forma:
Nesse exercício, como temos regime permanente, então podemos desconsiderar o termo com a derivada no tempo. Iremos desprezar também as forças de campo na direção , de modo que . Então a equação se torna:
Nesse caso, como estamos usando pressões manométricas, então . Sabemos também que e que , então, reescrevendo a equação, temos:
Substituindo os valores conhecidos: