Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 2.Problemas - Ex. 128
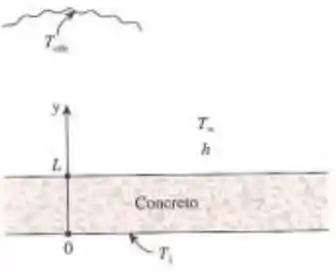
O telhado de uma casa é feito de laje de concreto de 25 cm de espessura, 8 m de largura e 10 m de comprimento . A emissividade da superfície externa do telhado é 0,8, e o coeficiente de transferência de calor por convecção nessa superfície é estimado em . Em uma noite clara de inverno, o ar ambiente encontra-se a uma temperatura de 10 °C, enquanto a temperatura do céu noturno para transferência de calor por radiação é 170 K. Considerando que a temperatura da superfície interna do telhado é , determine a temperatura da superfície externa do telhado e a taxa de perda de calor através do telhado quando condições de operação permanente são alcançadas.
Passo 1
Vamos lá! Nosso ponto de partida é entender quais as condições que o nosso problema está sujeito, isto é, quais são as nossas hipóteses!
Temos um problema de calor unidimensional em regime permanente, sem geração de calor, com condutividade térmica constante e com o efeito de radiação. Além disto, estamos trabalhando com um telhado retangular.
Agora, podemos iniciar a questão em si! Queremos determinar a temperatura na superfície externa, isto é, . Mas como faremos? Para isto, precisamos escrever as condições de contorno na superfície externa. Desta forma, temos:
Tirando o termo , temos todos os dados acima (claro que não temos , pois é ele quem queremos determinar). Então, como conseguiremos determinar esta derivada?
Passo 2
É neste ponto que utilizamos as nossas hipóteses. Por causa delas, sabemos que a distribuição de temperatura é linear. Sendo assim, aproximamos a derivada por deltas! Agora, basta resolvermos a nossa equação!
Agora, precisamos utilizar um algum método iterativo para resolver a equação acima, pois temos termos elevado a 4! Outro detalhe importante de ser observado é que quando estamos falando sobre radiação, a nossa temperatura tem que estar em Kelvin! Sendo assim, somamos 273 a temperatura em graus Celsius.
Resolvendo a nossa equação, vamos obter que a temperatura na superfície externa é aproximadamente:
E esta é a nossa resposta
Passo 3
Para finalizar, precisamos calcular a taxa de transferência de calor através do telhado. Para isto, basta aplicarmos diretamente na fórmula. Logo,
Resposta
A temperatura na superfície externa é:
Já a taxa de transferência de calor é: