Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 2.Problemas - Ex. 129

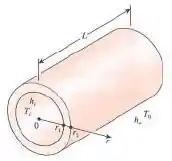
Considere uma tubulação de vapor de comprimento L, raio interno r 1 , raio externo r 2 e condutividade térmica k . Vapor flui dentro do tubo a uma temperatura média T i , com coeficiente de transferência de calor por convecção h i . A superfície externa da tubulação está exposta à convecção para o ar ambiente a uma temperatura T 0 , com coeficiente de transferência de calor h 0 . Assumindo que a condução de calor através do tubo é unidimensional e permanente, (a) expresse a equação diferencial e as condições de contorno para a condução de calor através do tubo, (b) obtenha a relação para a variação da temperatura no tubo resolvendo a equação diferencial e (c) obtenha a relação para a temperatura na superfície externa do tubo.

Passo 1

Vamos lá! Nosso ponto de partida é entender quais as condições que o nosso problema está sujeito, isto é, quais são as nossas hipóteses!

Temos um problema de calor unidimensional em regime permanente, sem geração de calor e com condutividade térmica constante.

Como estamos trabalhando com um cilindro, vamos utilizar o sistema de coordenadas cilíndrico. Portanto, temos a seguinte equação diferencial que rege o nosso problema:

1 r d d r r d T d r = 0

Agora, vamos descrever as condições de contorno do nosso problema. Como temos, convecção em ambas as superfícies, as condições de contorno são:

- k ∂ T ∂ r r = r 1 = h i T i - T r 1

- k ∂ T ∂ r r = 2 = h 0 T r 2 - T 0

Passo 2

Agora, vamos resolver a nossa EDO. Integrando-a duas vezes, temos:

1 r d d r r d T d r = 0 ⟹ d d r r d T d r = 0

r d T d r = C 1 ⟹ d T d r = C 1 r

T r = C 1 ln ⁡ r + C 2

Para podermos finalizar a equação que define a variação de temperatura, precisamos descobrir quem são as suas duas constantes. Para isto, utilizaremos as condições de contorno do nosso problema. Logo,

- k C 1 r 1 = h i T i - C 1 ln ⁡ r 1 + C 2

- k C 1 r 2 = h 0 C 1 ln ⁡ r 2 + C 2 - T 0

Da primeira equação obtemos:

C 2 = T i - C 1 ln ⁡ r 1 - k r 1 h i

Substituindo na segunda equação e isolando C 1 , descobrimos que esta constante é dada por:

C 1 = T i - T 0 ln ⁡ r 1 r 2 - k r 1 h i - k r 2 h 0

E consequentemente, conseguimos descobrir quem é C 2 . Substituindo ambas as constantes na equação da variação de temperatura, temos:

T r = T i - T 0 ln ⁡ r 1 r 2 - k r 1 h i - k r 2 h 0 ln ⁡ r + T i - T i - T 0 ln ⁡ r 1 r 2 - k r 1 h i - k r 2 h 0 ln ⁡ r 1 - k r 1 h i

T r = T i - T 0 ln ⁡ r 1 r 2 - k r 1 h i - k r 2 h 0 ln ⁡ r r 1 + k r 1 h i + T i

E assim respondemos o nosso item b).

Passo 3

Por fim, precisamos obter a temperatura na superfície externa do tubo. Para isto, basta substituirmos r = r 2 na equação encontrada no final do Passo 2. Logo, temos:

T r 2 = T i - T 0 ln ⁡ r 1 r 2 - k r 1 h i - k r 2 h 0 ln ⁡ r 2 r 1 + k r 1 h i + T i

Resposta

  1. A equação diferencial e as condições de contorno são:

    2. 1 r d d r r d T d r = 0

    - k ∂ T ∂ r r = r 1 = h i T i - T r 1

    - k ∂ T ∂ r r = 2 = h 0 T r 2 - T 0

  2. A variação de temperatura no tubo é:

    3. T r = T i - T 0 ln ⁡ r 1 r 2 - k r 1 h i - k r 2 h 0 ln ⁡ r r 1 + k r 1 h i + T i

  3. A temperatura na superfície externa é:

T r 2 = T i - T 0 ln ⁡ r 1 r 2 - k r 1 h i - k r 2 h 0 ln ⁡ r 2 r 1 + k r 1 h i + T i

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Reconsidere o Prob. 2-105. Usando EES (ou outro programa), trace a taxa de condução de calor através da placa como função da temperatura do lado quente da placa no intervalo de 400 K a 700 K. Discuta
Reconsidere o Prob. 2-94. Usando a relação fornecida para o calor gerado na parede, trace a geração de calor como função da distância x no intervalo de x = 0 a x = L e discuta os resultados obtidos. U
Considera a função f x , y e sua derivada parcial ∂ f / ∂ x . Sob quais condições essa derivada parcial seria igual à derivada ordinária d f / d x ?
Quando a condutividade térmica do meio variar linearmente com a temperatura, podemos afirmar que a condutividade térmica média será sempre equivalente ao valor da condutividade em temperatura média?
Considere uma parede plana de espessura L cuja condutividade térmica varia no intervalo específico de temperaturas, com k T = k 0 1 + β T 2 , onde k 0 e β são duas constantes especificadas. A superfíc