13. A taxa de transferência de calor, por unidade de largura (normal à página), em uma seção longitudinal, x2 – x1, pode ser representada por = 12 (x2 – x1)(Ts – T∞), sendo 12 o coeficiente médio na seção de comprimento (x2 – x1). Considere escoamento laminar sobre uma placa plana com uma temperatura uniforme Ts. A variação espacial do coeficiente convectivo local tem a forma hx = Cx−1/2, sendo C uma constante.
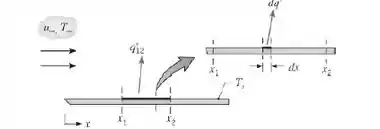
(a) Partindo da equação da taxa convectiva na forma dq′ = hx dx(Ts – T∞), deduza uma expressão para 12 em termos de C, x1 e x2.
(b) Deduza uma expressão para 12 em termos de x1, x2 e dos coeficientes médios 1 e 2, correspondentes aos comprimentos x1 e x2, respectivamente.
Passo 1
Letra (a)
A taxa total de transferência de calor é obtida através da integração do fluxo local sobre a superfície.
Nesse sentido, temos
O fluxo de calor local é expresso como
Ao substituir (2) por (1), temos
É dado que a transferência de calor ocorre ao longo de uma seção longitudinal . Portanto, (3) pode ser reescrito como,
A taxa de transferência de calor da seção é expressa como
Ao equacionar a equação (4) e a equação (5), temos
O coeficiente de convecção local é (dado)
Substituindo em (6), temos
Ao integrar, temos,
Ao aplicar os limites, temos,
Portanto, o coeficiente médio de transferência de calor é,
Passo 2
Letra (b)
A equação (5) pode ser reescrita usando as condições como,
Em 1 ,
Em ,
Portanto, a equação (5) produz,
Ao equacionar a equação (5) e a equação (6), temos,
Daí coeficiente médio de convecção em termos de é,