O teorema de transporte de Reynolds (TTR) é discutido no Capítulo 4. Para o caso geral de um volume de controle móvel c/ou deformável, escrevemos o TTR da seguinte maneira:

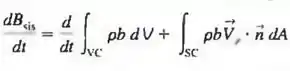
onde é a velocidade relativa, ou seja, a velocidade do fluido relativa à superfície de controle. Escreva as dimensões primárias de cada termo aditivo da equação e certifique-se de que a equação é dimensionalmente homogénea. Mostre todo o seu trabalho. (Sugestão: como B pode ser qualquer propriedade do escoamento — escalar, vetorial ou mesmo tensional — ele pode ter uma variedade de dimensões. Assim, basta deixar que as dimensões de B sejam aquelas do próprio B {B}. Da mesma forma, b é definido como B por unidade de massa.)

Oi pessoal, tudo bem?

Primeiro, vamos pontuar as dimensões primárias que já conhecemos:

1. As dimensões primárias da derivada do tempo são ;

2. As dimensões primárias da densidade são ;

3. As do volume são ;

4. As da área são ;

5. E as da velocidade são ;

6. A dimensão primária do vetor é unitário, {1} (em outras palavras, não tem dimensões);

7. Finalmente, as dimensões primárias de b, que é definido como B por unidade de massa (como o problema mostrou), são {}.

Vamos agora ver se a equação é dimensionalmente homogênea.