Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 13

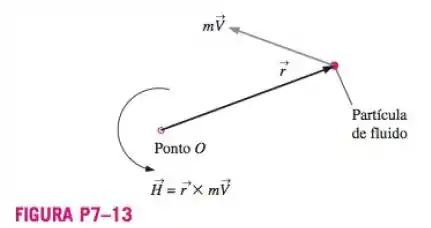
O m o m e n t o   a n g u l a r , também chamado de m o m e n t o   d o   m o m e n t o   H → , é formado pelo produto vetorial de um braço de momento r → e pelo momento linear m V → de uma partícula de fluido, conforme representação da Figura P7-13. Quais são as dimensões primárias do momento angular? Liste as unidades do momento angular em unidades S I primárias e em unidades inglesas.

Passo 1

Temos que determinar as unidades do momento angular na forma primária, SI e unidades inglesas.

Primeiramente vamos determinar as grandezas da fórmula do momento angular:

H → = r → × m V →

Temo que r é raio do centro de eixo ao ponto que está a partícula.

m é a massa da partícula.

V é a velocidade da partícula.

H = c o m p r i m e n t o ∙ m a s s a ∙ c o m p r i m e n t o t e m p o

Escrevendo em unidades primárias:

H = L ∙ m ∙ L t

H = L 2 t m

Passo 2

Temos que transformar as unidades do momento angular no Sistema internacional de unidades.

Para isto temos a seguinte fórmula:

H = c o m p r i m e n t o ∙ m a s s a ∙ c o m p r i m e n t o t e m p o

Para o S I comprimento é em metros, massa em k g e tempo em segundos, portanto:

H = m ∙ k g ∙ m s

H = m 2 s k g

Passo 3

Temos que transformar as unidades do momento angular no Sistema de unidades inglesas.

Para isto temos a seguinte fórmula:

H = c o m p r i m e n t o ∙ m a s s a ∙ c o m p r i m e n t o t e m p o

Para as unidades inglesas comprimento é em pés, massa em l b m e tempo em segundos, portanto:

H = f t ∙ l b m ∙ f t s

H = f t 2 s l b m

Resposta

Unidades primárias:

H = L 2 t m

Sistema internacional:

H = m 2 s k g

Unidades inglesas:

H = f t 2 s l b m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O número de Richardson, Ri, que correlaciona a produção de turbulência pela flutuabilidade, é uma combinação adimensional da aceleração da gravidade g , da temperatura do fluido T 0 , do gradiente loc
Durante a II Guerra Mundial, Sir Geoffrey Taylor, um estudioso britânico da dinâmica dos fluidos, usou a análise dimensional para calcular a energia liberada pela explosão de uma bomba atômica. Ele su
Para o escoamento permanente a baixa velocidade (laminar)através de um tubo circular, como representa a Figura P1.12, a velocidade u varia com o raio e assume a forma u = B Δ p μ ( r 0 2 - r 2 ) em qu
Suponha que saibamos pouco sobre a resistência dos materiais, mas nos informaram que a tensão de flexão σ em uma viga é proporcional à metade da espessura y da viga e também depende do momento de flet
Mott [49] recomenda a seguinte fórmula, no sistema inglês, para a perda de carga por atrito h P , em f t , para um escoamento através de um tubo de comprimento L e diâmetro D (ambas as medidas devem e